4.3. Обратная решётка

Решётка Браве задаётся вектором решётки , где базисные векторы решётки, n_i – целые числа. Этой решётке соответствует обратная решётка, которая задаётся вектором

, (11)

где т_j – целые числа, базисные векторы обратной решётки, которые связаны с базисными векторами решётки Браве условием ортогональности

. (12)

Из условия (12) следует, что и базисный вектор обратной решётки соответственно имеет размерность , совпадающей с размерностью волнового вектора (и квазиволнового вектора). Поэтому обратная решётка является решёткой в k-пространстве.

Вычислим скалярное произведение векторов прямой и обратной решётки, т.е. .

Поскольку n_i и m_i – целые числа и сумма их произведения также есть целое число поэтому , а следовательно

(13)

Условие (13) можно рассматривать как одно из определений обратной решётки.

4.4. Неоднозначность квазиимпульса

Запишем теорему Блоха в первой формулировке

.

Умножим правую часть на множитель , равный единице согласно условию (13): таким образом,

, (14)

т.е. состояния электрона с и физически эквивалентны. Поэтому квазиволновой вектор определён с точностью до вектора обратной решётки, а соответственно квазиимпульс с точностью до вектора .

4.5. Приведение к первой зоне Бриллюэна

Рассмотрим, для простоты, одномерный кристалл с межатомным расстоянием а. В одномерном случае модуль вектора обратной решётки есть , где базисный вектор , т.е.

, (15)

где т – целое число. Так как вектор обратной решётки имеет размерность волнового вектора, то его можно использовать как вектор трансляции в -пространстве. Особыми точками в одномерном k-пространстве являются точки , где п – целое число. Эти точки являются границами зон Бриллюэна, при таких значениях k в кристалле происходит брэгговское отражение (в случае электронов – блоховских волн). Размер каждой зоны Бриллюэна равен . Поэтому модуль вектор обратной решётки равен целому числу размеров зоны Бриллюэна. Из свойства неоднозначности квазиимпульса следует, что всегда можно найти такое целое число т, чтобы любому квазиволновому вектору сопоставить ему физически эквивалентный в 1-ой зоне Бриллюэна, т.е. в интервале от / до / (Рис. 4.1.).

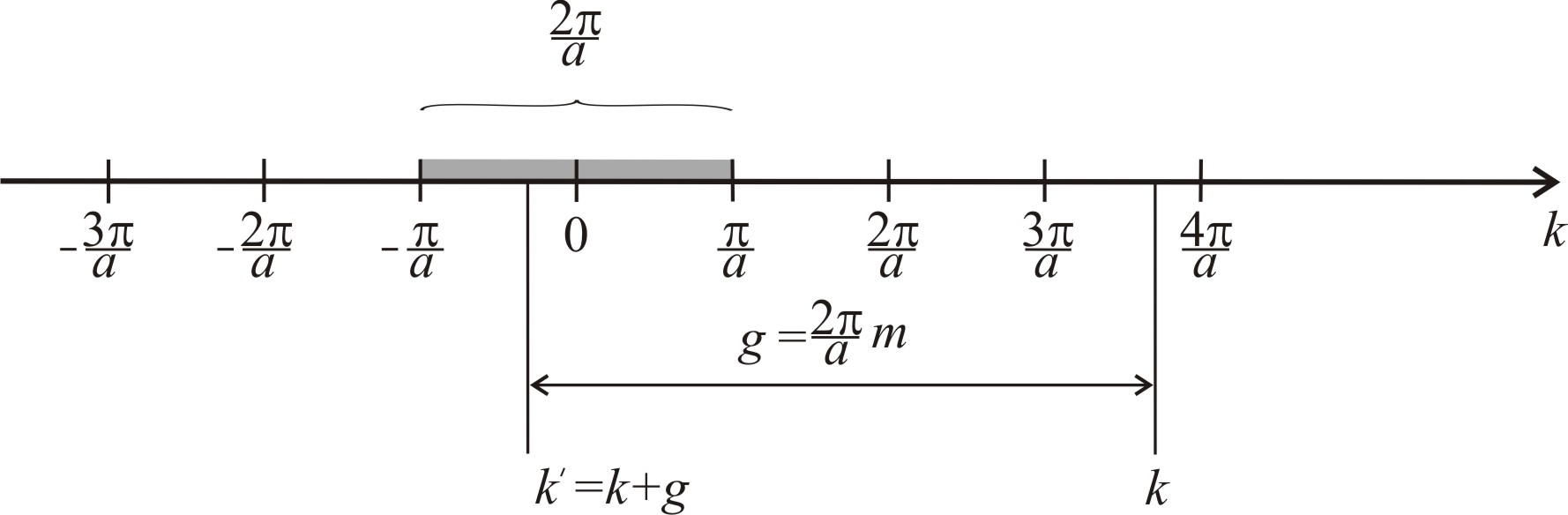
Рис. 4.1. Схема, поясняющая приведение к 1-ой зоне Бриллюэна для одномерного кристалла

Таким образом, в 1-ой зоне Бриллюэна находятся все физически неэквивалентные квантовые состояния электрона в кристалле. Для того, чтобы вычислить количество таких состояний, необходимо принять во внимание, что в кристалле конечных размеров (потенциальной яме для электронов) значения k принимает дискретный ряд значений.

4.6. Количество состояний в зоне Бриллюэна

Рассмотрим движение электрона в одномерном кристалле размером L_x и межатомным расстоянием а. Мысленно свернём эту цепочку атомов в окружность, соединив первый и последний атомы, и сошьём решения (блоховские состояния электрона) на границе

. (16)

Подставляя в эти граничные условия одномерную функцию Блоха , где u(x)=u(x+R), а вектор решётки R=na , получим:

. (17)

Поскольку размер кристалла L_x=N_атa является вектором решётки, то u(x)=u(x+L_x) и из (17) получим:

. (18)

Решая это уравнение, имеем

, где т – целое число.

Таким образом, значения k_x квантуется, т.е. принимают дискретный ряд значений, а на одно квантовое состояние приходится отрезок k_x-оси, равный

.

Аналогично используем циклические граничные условия по осям y и z:

,

и получим: и . В трёхмерном случае на одно квантовое состояние будет приходиться объём k-пространства, равный

, (19)

где V=L_xL_yL_z – объём кристалла.

Теперь можно вычислить количество физически различных состояний в 1-ой зоне Бриллюэна, как отношение объёма зоны к объёму k-пространства, приходящееся на одно квантовое состояние.

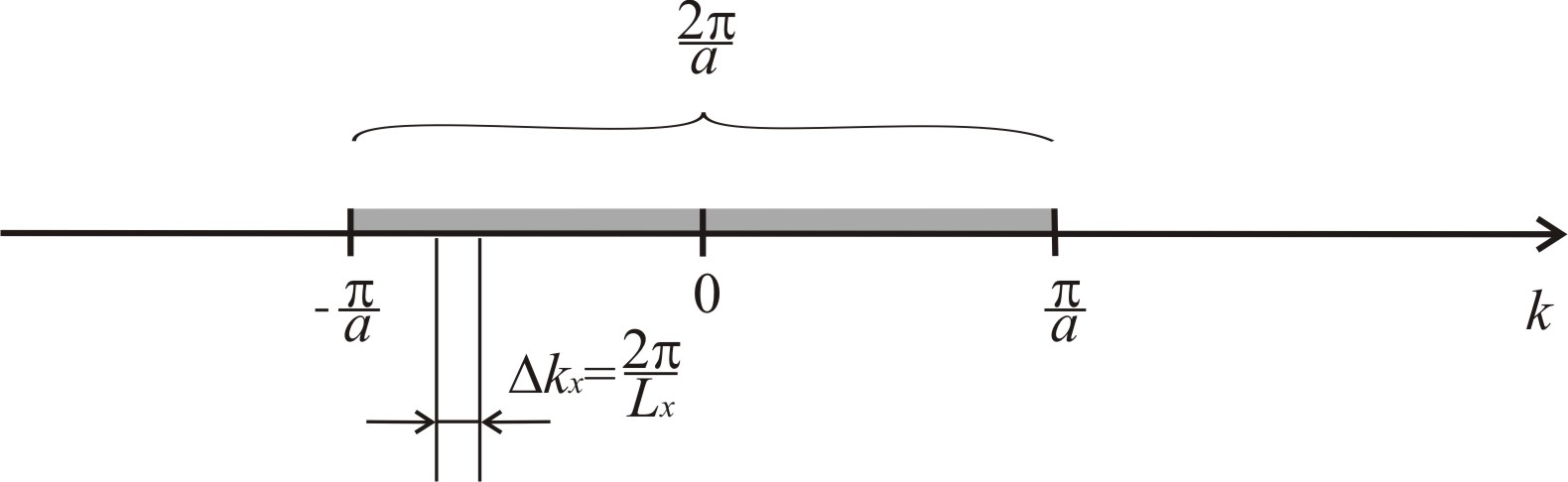
Рис.  4.2. К расчету числа состояний в 1-ой зоне Бриллюэна

В одномерном случае объём зоны Бриллюэна равен , а объём на одно состояние , поэтому полное число состояний

. (20)

Таким образом, количество квантовых состояний в 1-ой зоне Бриллюэна (и в любой другой) равно числу элементарных ячеек кристалла N_яч. Такой же результат, очевидно, получится для двух- и трёхмерного кристалла.

Подведём итог исследований основных свойств электронных состояний в идеальном кристалле. В соответствие с теоремой Блоха состояние электрона в периодическом поле кристаллической решётки определяется плоской блоховской волной , амплитуда которой является периодической функцией . Эта функция является одновременно собственной функцией одночастичного оператора Гамильтона кристалла и оператора квазиимпульса , т.е.

. (21)

Поэтому интегралами движения электрона в кристаллической решетке являются полная энергия и квазиимпульс , который классифицирует собственные функции и собственные значения энергии .

В отличие от обычного импульса квазиимпульс неоднозначен, так как состояния с и физически эквивалентны:

,

а следовательно:

, (22)

т.е. зависимость энергии электрона от квазиволнового вектора – закон дисперсии – является периодической функцией в k-пространстве с периодом равным вектору обратной решётки. Так как модуль вектора обратной решётки кратен размеру зоны Бриллюэна, то зависимость обычно рассматривают лишь в первой зоне Бриллюэна, где энергия электрона является однозначной функцией k. Для кристалла конечных размеров величина k квантуется и соответственно энергия электрона принимает дискретный ряд значений от некоторого минимального значения E_min до максимального Е_mах. Количество уровней равно полному количеству состояний в 1-ой зоне Бриллюэна, т.е. количеству элементарных ячеек кристалла. Таким образом, спектр энергии электрона заключён в интервале (разрешённой зоне) и имеет в этом интервале дискретный характер.

Для кристалла размером ~ 1 см число ячеек N_яч~10²²-10²³. Так как характерные энергии электронов в кристаллах порядка 1-10 эВ, то расстояние между уровнями в зоне ~ 10^-21-10^-22 эВ, что соответствует квазинепрерывному спектру. Подход, основанный на анализе свойств симметрии потенциального рельефа кристалла, позволяет качественно понять, что спектр энергии электрона в кристалле носит зонный характер, т.е. состоит из разрешённых энергетических зон, количество уровней в которых равно числу элементарных ячеек кристалла.