26. Бір бағыттас тербелістерді қосу(соғу құбылысы). Бір-біріне көлденең бағыттас тербелістерді қосу.(Лиссажау фигуралары)

Тербелістер деп əртүрлі қайталанушылық дəрежесімен ерекшеленетін

үрдістерді атайды. Қайталанушылықтың мұндай қасиетіне мысалы, сағат

маятнигінің тербелісі, шек тербелесі немесе, камертон аяқтары,

радиоқабылдағыш контурындағы конденсатор орамалары арасындағы кернеу

ие бола алады.

Қайталанушы үрдістің физикалық табиғатына қарай тербелістер мынадай

түрлерге бөлінеді: механикалық, электромагниттік, т.б.

Тербелуші жүйеге тигізетін əсерінің сипатына қарай еркін (немесе

меншікті) тербелістер, еріксіз тербелістер, автотербелістер жəне

параметрлік тербелістерді кездестіреміз.)

Тербелістердің қосылуы. Соғулар. Бір бағыттағы екі қосылушы

гармониялық тербелісті жиілігі бойынша бір бірінен аса айырмашылығы

бола қоймайтын жағдайда қарастырайық. Осы үрдіс практикада ерекше

қызығушылық тудырады. Мұндай жағдайда қорытқы қозғалысты

амплитудасы пульсацияланатын гармониялық тербеліс ретінде қарастыруға

болады. Мұндай тербелістер соғулар деп аталады.

Ұзын жіңішке жіпке іліген ауыр шарикты қарастырайық.Бұл шарик бір біріне перпендикуляр бағытта екі тербеліс жасай алады, сонымен қатар екі тербелістің жиілігі бір біріне дәл келеді.Бұл жағдайда шарик формасы екі тербелістің фазалар айырмасына тәуелді болатын кейбір қисық сызық траекториясының бойымен қозғалады. X және y координата остерінің бойымен бірдей ὠ жиілікпен тербелетін өз ара перпендикуляр екі тербелісті қосуға көшейік. Бастапқы фазасы нөл деп алсақ:

x=acoswt, y=cos(wt+a)

a-екі тербелістің фазалары айырмасы.Егер онша күрделі емес түрлендірулерден кейін соңғы тендей алуға болады

X²/y²+y²/b²-(2xy/ab)(cosa)=sin²a

1. Егер фазалар айырмасы нолге тең болса бұл теңдеу былай өзгереді: [(x/a)-(y/b)]²=0

2. Ал егер фазалар айырмасы 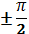болғанда: [(x/a)+(y/b)]²=1, a,b амплитудалары тең болса шенберге айналады

a фазалар айырмасы : [(x/a)+(y/b)]²=0

егер өз ара перпендикуляр тербелістердің жиіліктері бірдей болмаса, онда қорытқы қозғалыстың траекториясы лисажу фигуралары дер аталатын өте күделі қисық түрде болады.Мысалға нүкте х осі бойымен бір шектік жағдайдан екінші жағдайға орын ауыстып үлгергенше у осі бойымен нольдік қалыпта шыға отырып, бір шектік жағдайда, сонан соң, екіншісіне келіп және нольдік жағдайға жетіп үлгереді.

Жиіліктері 1:2 қатынасындай және фазалар айырмасы нольге тең болғанда траектория бойымен қозғалған нүкте бір ұшына барып, қайта қайтатын қисық сызыққа айналады.Тербеліс жиіліктерінің қатынасын өрнектейтін рационал бөлшек неғұрлым бірге жақындаған сайын, соғұрлым Лиссажу фигуралары да күрделенеді.

27. Гироскоп. Гироскоптың прецесиясы.

Гироскоп(немесе зырылдауық) деп, симметрия осінен өте зор жылдамдықпен айналатын шомбал симметриялы денені айтады.Симметрия өсі гироскоп инерциясының бас өстерінің бірі болып табылады, сондықтан гироскоп импульсінің бағыты бойынша айналу өсімен дәл келеді. Тікелей аударғанда гироскоп айналуды табатын аспап деген мағынаны береді. Гироскопқа мысал ретінде зырылдауықты, центрі арқылы өткен, бетіне перпендикуляр өсте өте тез айналған дискіні келтіруге болады. Гироскоптық тез айналумен байланысты барлық құбылыстар гироскоптық деп аталады.

Гироскоп:

1. Орнықты – инерция моменті максимум, минимум мәндерге ие болса.Гироскоп орнықты болу үшін тірек нүктесі массалық центрмен сәйкес болу керек. Массалық центрді тірек нүктесінен ауытқытып жіберсек прецессия қозғалысы туындайды.

2. Орнықты емес- еркін осьтердің маңайындағы қозғалысы.

Гироскоп прецессиясы.

Прецессия қозғалыс күш моменттердің туындауына байланысты гироскоптың айналу өсінің басқа бір өсінің маңайында белгілі бір жазықтыққа айналады.Мутация- гироскоптың бұрыштық жылдамдық векторының симметрия өсінің маңайында конус бет жасап қозғалуы.Гироскопқа түсірілген сыртқы күштердің моменті шамасы бойынша мынаған тең: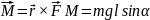

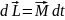
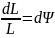
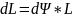
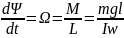
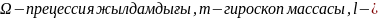топсадан гироскоптың инерция центріне дейінгі арақашықтық, 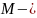моменті гироскоп өсі арқылы өтетін вертикаль жазықтыққа вертикаль бaғытталған.

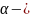гироскоп өсі мен вертикаль арасында пайда болған бұрыш. Гироскоптың импульс моменті күш моментінің әсерімен dt уақыт ішінде

өсімшесін алады, бұл өсімше бағыты бойынша М векторымен дәл келеді, яғни L

векторына перпендикуляр болады.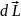 өсімшесін алғаннан кейін, L векторының алған өзгерісі гироскоп өзгерісінің түзуінен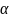 бұр ышының өзгермейтін бұрылысына сәйкес келеді.

28. Гармониялық тербелістердің болу шарттары және гармониялық тербеліс теңдеуі. Гармониялық осцилятордың қозғалысын сипаттайтын физикалық шамалар. Бастапқы шарттырдың ролдері.

Ең қарапайымы болып гармонияық тербелістер саналады, яғни тербеліс кезінде тербелуші шама уақыт өте келе синус жəне косинус заңымен өзгереді. Тербелістердің бұл түрі əсіресе мына себептерге байланысты аса маңызды: біріншіден, тербелістер табиғатта жəне техникада гармониялық түрге өте жақын сипатта болады, жəне, екіншіден, бөтен формадағы периодтық үрдістер бірнеше гармониялық тербелістердің қабаттасуы ретінде көрінуі мүмкін.

Гармониялық осциллятор. Дененің күш əсерімен тербелуі үрдісін сандық жағынан сипаттау үшін Ньютон механикасы заңдарын пайдалану қажет. Серіппенің серпімділік күші əсерінен тербелуші дененің (мысалы домалақ шар) қозғалысын қарастырайық (F = - kx). Үйкеліс күшінің

қозғалысқа тигізетін əсерін есепке алмаймыз.Шарик үшін Ньютонның екінші заңының теңдеуі мына түрде болады:т mx= −kx , (155)

мұнда x – тепе-теңдік қалпына дейінгі қашықтық ал k – серіппенің қатаңдығы. (155) түріндегі теңдеу гармониялық тербелістер теңдеуі деп аталады, ал осы кіші тербелістерді іске асырушы жүйе сызықтық немесе гармониялық осциллятор деп аталады. Осылайша, серіппеде тербелуші дене сызықтық осциллятор моделі боп табылады. Сызықтық осциллятордың басқадай мысалы ретінде ауытқу бұрышы жеткілікті түрде аз болатын физикалық жəне математикалық маятниктерді қарауға болады.

Сонымен, үйкеліс күші жоқ кезде серпімді күш əсеріндегі қозғалыс (156) дифференциалды еңдеумен сипатталады. Бұл теңдеу гармониялық тербелістер теңдеуі деп аталады. (156) теңдеуінің жалпы шешімі мынадай:

x = a cos (w t +ϕ ) , (157)

мұнда a мен ϕ – еркін тұрақтылар. a шамасы амплитуда деп, w – гармониялық тербелістің дөңгелек немесе циклдіқ жиілігі, ал косинус аргументінде тұрған w t +ϕ шама – тербеліс

фазасы деп аталады. ϕ фазаның t=0 болғандағы мəнін бастапқы фаза дейді. х-косинус заңы бойынша өзгереді, ендеше дененің тербелісі гармоникалық тербеліс.

Фаза берілген амплитуда кезінде кез келген уақыт мезеті үшін тербелмелі жүйенің күшін анықтауға болады.

Фаза:

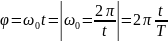
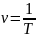тербеліс жиілігі(бірлік уақытындағы тербеліс саны)

Бастапқы шарттар. Гармониялық тербеліс толығымен жиілікпен, амплитудамен жəне бастапқы фазамен сипатталады. Жиілік жүйенің физикалық қасиеттерінен тəуелді. Амплитуда мен тербелістің бастапқы фазасын анықтау үшін материялық нүктенің қандай – да бір уақыт мезетіндегі орны мен жылдамдығын білу керек.

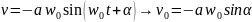
Осы екі теңдеуден белгісіз амплитуда мен бастапқы фазаны есептейді.

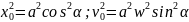
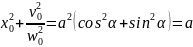
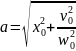
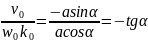
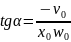
Жылдамдық пен үдеудің өзгерістері. Гармониялық осциллятордың энергиясы. (157)-ні уақыт бойынша дифференциалдап, жылдамдықта гармониялық заң бойынша өзгеретінін көрсетуге болады. Салыстыру көрсеткендей, жылдамдық ығысуды фаза бойынша π / 2 -ге алдын орап

о тырады. (157) - ні уақыт бойынша екі рет дифференциалдап үдеу үшін өрнекті табуға болады. Анализ көрсететіндей, үдеу мен ығысу қарама-қарсы фазада болады.

Квазисерпімді күш консервативті болып табылады. Сондықтан гармониялық тербелістің толық энергиясы тұрақты болып қалуы керек. Толық энергия үшін формула: