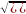- •1 Билет. Қисықсызықты қозғалыстардың жылдамдығы , үдеуі. Бұрыштық жылдамдық пен бұрыштық үдеу векторлары
- •2 Билет. Галилей түрлендірулері. Галилей түрлендірулерінің инварианттары
- •4 Билет. Релятивистік механикадағы уақыттық-кеңістіктік интервалдың инварианттылығы. Релятивистік механикадағыменшікті уақыттың инварианттылығы.
- •Таяқшаның ұзындығының инварианттылығы. Уақыт аралық интервалдың инварианттылығы. Үдеудің инварианттылығы
- •7. Материялық нүктенің қозғалысы үшін моменттер теңдеуі. Матер.Нүктелр.Жүйесі үшін моменттер теңдеуі.
- •8. Материялық нүктелер жүйесінің қозғалысы. М.Н жүйесіне әсер ететін күш моменті. Материялық нүктелер жүйесінің массалар центрі.
- •9 Билет. Нормаль және тангенциал үдеулер, толық үдеу.
- •11. Ньютон заңдары. Ауырлық күші. Салмақ. Ньютонның Бүкіләлемдік тартылыс заңы
- •12. Классикалық механикадағы жылдамдықтарды қосу формулалары. Релятивистік механикадағы жылдамдықтарды қосудың формулалары.
- •13. Релятивистік қозғалыстарға Галилей түрлендірулерінің қолдануға болмайтындығы. Лоренц түрлендірулері.
- •14. Лоренц түрлендірулерінің инварианттары.
- •15. Массасы айнымалы дененің қозғалысы. Мещерский теңдеуі.
- •16. Материялық нүктелер жүйесі үшін импульстің сақталу заңы. Материялық нүктелер жүйесінің импульс моментінің сақталу заңы.
- •17. Материялық нүктелер жүйесінің қозғалысы. Материялық нүктелер жүйесіне әсер ететін күш .Сыртқы күш.
- •18. Күш жұмысы. Потенциялық күштер. Потенциялық өріс күшінің жұмысы. Потенциялық энергияны нормалау. Энергияның сақталу заңы.
- •20. Кеплердің 1,2 және 3 заңдары. Космостық жылдамдықтар.
- •22. Өске қатысты инерция моментін есептеу(таяқша). Гюйгенс-Штейнер теоремасын қорыту.
- •23. Инерциялық емес санақ жүйелері: Ілгермелі үдеумен қозғалатын жүйедегі инерциялық күштер. Айналмалы қозғалыстағы инерциялық емес санақ жүйелері. Центрден тепкіш күш.Кориолис күші.
- •24. Идеал сұйықтың стационар ағысы. Үзіліссіздік теңдеуі. Бернулли теңдеуін қорыту, оның қолданылу шарттары. Гидростатика заңдары.
- •25. Денелердің тұтқыр сұйық ішінде қозғалысы. Тұтқыр сұйық ішінде шариктің тұрақталған жылдамдықпен қозғалысы. Стокс заңы. Пуазейль формуласын қорыту.
- •26. Бір бағыттас тербелістерді қосу(соғу құбылысы). Бір-біріне көлденең бағыттас тербелістерді қосу.(Лиссажау фигуралары)
- •29.Жұмыс және кинетикалық энергия.Потенциялық емес күштердің жұмысы.
1 Билет. Қисықсызықты қозғалыстардың жылдамдығы , үдеуі. Бұрыштық жылдамдық пен бұрыштық үдеу векторлары
Егер материалдық нүкте қозғалғанда оның траекториясы қисық сызық болып келсе, онда қозғалыс қисық сызықты қозғалыс деп аталады. Енді осы қисық сызықты қозғалыскезіндегі жылдамдықпен үдеудің өзгерісін қарастырайық.
|
|
|
|
Қисық сызықты қозғалыс кезінде жылдамдық векторы берілген әрбір уақыт мезетінде дене траекториясына қозғалыстың бағыты бойынша жүргізілген жанама бойыменбағытталады. Дененің MN қисық сызығының бойымен қозғалысын қарастырайық.(4-сурет).
|
|
|
|
Айталық M және N нүктелеріндегі қозғалыс жылдамдықтары ![]() және
және ![]() болсын. Ал M нүктесіндегі үдеу (1.2.9) өрнекке сәйкес мына шамаға тең.
болсын. Ал M нүктесіндегі үдеу (1.2.9) өрнекке сәйкес мына шамаға тең.
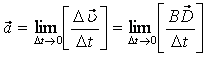 (1.3.1)
(1.3.1)
4
– суретте көрсетілгендей ![]() бойына
бойына ![]() -ға тең
-ға тең ![]() және
және ![]() кесінділерін аламыз. Сонда үдеуді былайша өрнектейміз:
кесінділерін аламыз. Сонда үдеуді былайша өрнектейміз:
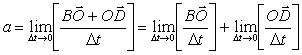 (1.3.2)
(1.3.2)
(1.3.2)- өрнектің екінші құраушысы 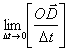 жанама немесе тангенциал үдеу деп аталады, себебі Δt→0 кезде OD кесіндісі M нүктесінің маңында айналып, траекторияныңжанамасымен беттесуге ұмтылады. Оның сан мәні мынаған тең:
жанама немесе тангенциал үдеу деп аталады, себебі Δt→0 кезде OD кесіндісі M нүктесінің маңында айналып, траекторияныңжанамасымен беттесуге ұмтылады. Оның сан мәні мынаған тең:
 (1.3.3)
(1.3.3)
Сонымен ![]() үдеу қозғалыс жылдамдығының сан жағынан өзгерісін көрсетеді. Кез келген бірқалыпты қозғалыс үшін
үдеу қозғалыс жылдамдығының сан жағынан өзгерісін көрсетеді. Кез келген бірқалыпты қозғалыс үшін ![]() болады. Ал (1.3.2)- өрнектің бірінші құраушысы
болады. Ал (1.3.2)- өрнектің бірінші құраушысы 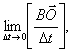 нормаль немесе центрге тартқыш үдеу деп аталады, себебі Δt→0 кезде Δt→0 да,
M нүктесіндегі
нормаль немесе центрге тартқыш үдеу деп аталады, себебі Δt→0 кезде Δt→0 да,
M нүктесіндегі ![]() жанамаға перпендикуляр болады. Сөйтіп, нормаль үдеудің сан мәнімына шамаға тең:
жанамаға перпендикуляр болады. Сөйтіп, нормаль үдеудің сан мәнімына шамаға тең:![]()
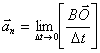
Енді ВО кесіндісінің мәні неге тең болатынын қарастырайық. ΔМВО-дан Δα бұрышын шексіз аз шама деп есептесек, ВО=MB Δα=vΔα, өйткені ![]() . Сонымен нормаль үдеудімына түрде жазуға болады:
. Сонымен нормаль үдеудімына түрде жазуға болады: ![]()
Бұл өрнектің оң жағын Δs–ке көбейтіп және бөлейік, сонда ол ![]() түрге келеді. Мұндағы Δs
–
MN доғасының ұзындығы. Егер геометрия курсынан қисықсызықтың қисықтығы деген ұғымды еске алатын болсақ, онда 4-суретке сәйкес Δs=RΔα . мұндағы R-қисықтық радиусы, Δα - центрлік бұрыш. Олай болса, Δα/ Δs=1/R және Mнүктесіндегі жылдамдық Δt уақыт өзгерісіне тәуелді болмайды.
түрге келеді. Мұндағы Δs
–
MN доғасының ұзындығы. Егер геометрия курсынан қисықсызықтың қисықтығы деген ұғымды еске алатын болсақ, онда 4-суретке сәйкес Δs=RΔα . мұндағы R-қисықтық радиусы, Δα - центрлік бұрыш. Олай болса, Δα/ Δs=1/R және Mнүктесіндегі жылдамдық Δt уақыт өзгерісіне тәуелді болмайды.
Сөйтіп 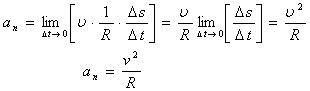 (1.3.4)
(1.3.4)
Сонымен, қисық сызықты қозғалыс кезінде нормаль үдеу қозғалыс жылдамдығы бағытының өзгерісін көрсетеді. Кез келген түзу сызықты қозғалыс үшін ![]() .
.
(1.3.1) теңдіктен материалдық нүктенің қисық сызықты қозғалысы кезіндегі толық үдеуі
оның нормаль және тангенциал үдеулері векторларының қосындысына теңекендігін көреміз: 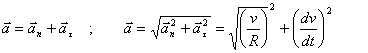 (1.3.5)
(1.3.5)
Толық үдеудің бағытын тангенциал үдеу мен толық үдеу немесе нормаль үдеу мен толық үдеу арасындағы бұрыш арқылы көрсетуге болады (5,6-сурет):
![]() (1.3.6)
(1.3.6)
Бұрыштық жылдамдық. Қатты дененің айналулары толығымен бұрыштық жылдамдықтың мəні арқылы сипатталады. Қатты дененің айналуларының барлық сипаттамаларын w бұрыштық айналу жылдамдығының векторы ұғымына біріктіруге болады.
Ол
модулі бойынша w=
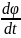 тең жəне V
қатты
дене нүктелерінің сызықтық
тең жəне V
қатты
дене нүктелерінің сызықтық
жылдамдығы
V = w × r (13)
формуласымен бейнеленетіндей жағдайда айналу өсінің бойымен
бағытталады.
Бұрыштық
үдеу.
Уақыт бойынша бұрыштық жылдамдықтың
туындысы
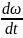
бұрыштық үдеу деп аталады:
Ɛ =
Ɛ-бұрыштық үдеу
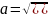 =
=
 =
=