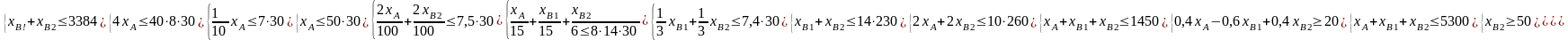- •Лекция 1 Литература для студентов Введение
- •Решение систем линейных уравнений
- •Методом обратных матриц
- •Метод наименьших квадратов
- •Основные теоретические положения задачи линейного программирования (злп)
- •Краткие сведения из теории злп Решение злп в табличном редакторе Microsoft Excel
- •Одноиндексные злп
- •Окно “Поиск решения” примера 1
- •Добавление условия неотрицательности переменных примера 1
- •Сообщение об успешном решении задачи
- •Сообщение при несовместной системе ограничении задачи
- •Сообщение при неограниченности цф в требуемом направлении
- •Двойственная задача
- •Двухиндексные злп
- •Экранная форма двухиндексной задачи
- •Типы отчетов в окне «Результаты поиска решения»
- •Типы отчетов в окне «Результаты поиска решения» Отчет по результатам
- •Отчет по устойчивости
- •Раздел 1 содержит информацию, относящуюся к переменной.
- •Раздел 2 содержит информацию, относящуюся к ограничению.
- •2.3.3. Отчет по пределам
- •Нелинейное программирование в Excel
- •Решение задачи про мебельные полки в Excel Пример 3. Задача про мебельные полки
- •2.4.2. Составление математической модели примера задачи про мебельные полки
- •1 Способ раскроя листа дсп 2х3 м2
- •2 Способ раскроя листа дсп 2х3 м2
- •3 Способ раскроя листа дсп 2х3 м2
- •2.4.3. Решение математической модели задачи про полки в табличном редакторе Microsoft Excel
- •2.4.4. Анализ чувствительности задачи про полки
- •Регрессионный анализ в Exsel
- •Нелинейные регрессионные уравнения
- •Компьютерный практикум по начальному курсу эконометрики (реализация на eviews)
- •9. Проверить спецификацию модели. Объяснить полученные результаты.
- •10. Проверить наличие гетероскедастичности в модели. Объяснить полученные результаты.
- •11. Оформить отчет.
1 Способ раскроя листа дсп 2х3 м2

2 Способ раскроя листа дсп 2х3 м2

3 Способ раскроя листа дсп 2х3 м2
Построим математическую модель оптимального раскроя листов ДСП.
Пусть у1, у2, у3 – объем листов ДСП раскроенных соответственно 1, 2, 3 – способами. Y – количество комплектов деталей раскроенных из ДСП для производства полок В1 и В2. Тогда модель примет вид (21):

Решение задачи раскроя листа ДСП получим с помощью редактора Microsoft Excel ( табл. 8)
Решение задачи раскроя листа ДСП
Переменные |
||||||
у1 |
у2 |
у3 |
Y |
|
|
|
9,00 |
115,00 |
276,00 |
3384,00 |
|
|
|
0 |
0 |
0 |
0 |
цф |
|
|
целое |
целое |
целое |
целое |
значение |
напр-е |
|
0 |
0 |
0 |
1 |
3384,00 |
max |
|
ограничения |
||||||
|
|
|
|
лев. ч. |
знак |
прав.ч. |
16 |
36 |
9 |
-2 |
0,00 |
= |
0 |
16 |
12 |
19 |
-2 |
0,00 |
= |
0 |
1 |
1 |
1 |
0 |
400,00 |
<= |
400 |
После решения задачи раскроя листа ДСП получаем первое ограничение (22)
1. Объем производства.[шт/мес].
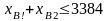
Для построения следующих 6 ограничений построим табл. 9 и запишем в виде неравенств (26) – (31).
|
№ |
вид работы |
вид опер. |
Тр[ч/п] |
Пр[п/ч] |
ФВ[ч/с] |
V[п/с] |
Р[чел] |
S[сут/м] |
A |
2 |
столяр. |
руч |
4 |
|
8 |
|
40 |
30 |
|
3 |
покр.лаком |
авт |
|
10 |
7 |
|
|
30 |
|
4 |
сушка лака |
авт |
|
|
|
50 |
|
30 |
|
5 |
резка стекла |
авт |
|
100 |
7,5 |
|
|
30 |
|
6 |
упаковка |
руч |
1/15 |
|
8 |
|
14 |
30 |
B1 |
6 |
упаковка |
руч |
2/15 |
|
8 |
|
14 |
30 |
|
7 |
компл. |
авт |
|
3 |
7,4 |
|
|
30 |
B2 |
5 |
резка стекла |
авт |
|
100 |
7,5 |
|
|
30 |
|
6 |
упаковка |
руч |
1/6 |
|
8 |
|
14 |
30 |
|
7 |
компл. |
авт |
|
3 |
7,4 |
|
|
30 |
2. Фонд времени по столярным работам. [ч/мес].
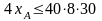
3. Сменный фонд по покрытию лаком. [ч/мес].
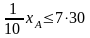
4. Сменный фонд по сушке. [шт/мес].
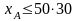
5. Сменный фонд по резке стекла. [ч/мес].
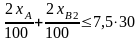
6. Сменный фонд по упаковке. [ч/мес].
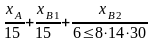
7. Фонд времени по производству комплектов В1, В2 [ч/мес].
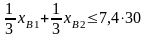
Остальные ограничения (29) – (35) записываем из оставшихся условий задачи:
8. Расход ДВП. [шт/мес].
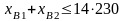
9. Расход стекла. [шт/мес].
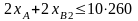
10. Емкость склада. [шт/мес].
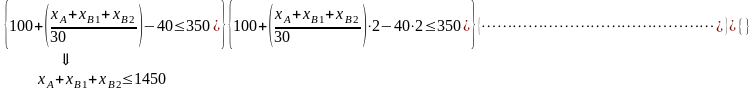
11. Доля продаж. [шт/мес].
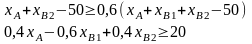
12. Емкость рынка. [шт/мес].
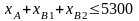
13. Заказ на полки B2 [шт/мес].

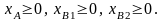
Математическая модель задачи про полки примет следующий вид (36):
Целевая функция:
Ограничения: