
Признак параллельности прямых
Теорема.
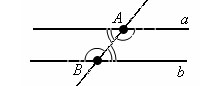 Если
внутренние накрест лежащие углы равны,
то прямые параллельны
Доказательство.
Пусть
прямые a и b образуют с секущей AB равные
внутренние накрест лежащие
углы.
Если
внутренние накрест лежащие углы равны,
то прямые параллельны
Доказательство.
Пусть
прямые a и b образуют с секущей AB равные
внутренние накрест лежащие
углы.
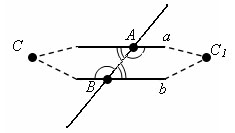 Допустим,
прямые a и b не параллельны, а значит,
пересекаются в некоторой точке С.
Отложим
от секущей AB треугольник ABC1, равный
треугольнику ABC, так, что вершина С1 лежит
в другой полуплоскости, чем вершина
С.
По
условию внутренние накрест лежащие
углы при параллельных прямых a, b и секущей
AB равны.
Из
равенства треугольников следует, что
∠
CAB = ∠
C1BA и ∠
CBA = ∠
C1AB и они совпадают с внутренними накрест
лежащими углами. Значит, прямая AC1
совпадает с прямой a, a прямая BC1 совпадает
c прямой b. Отсюда следует, что через две
различные точки С и С1 проходят две
различны прямые a и
b. Это противоречит аксиоме о том, что
«Через любые две точки можно провести
прямую, и только одну». Значит, прямые
параллельны.
Из
теоремы следует:
Две
прямые, перпендикулярные третьей,
параллельны.
На
основании теоремы доказывается:
Если
соответственные углы равны, то прямые
параллельны.
Если
сумма внутренних односторонних углов
равна 180°, то прямые параллельны.
Допустим,
прямые a и b не параллельны, а значит,
пересекаются в некоторой точке С.
Отложим
от секущей AB треугольник ABC1, равный
треугольнику ABC, так, что вершина С1 лежит
в другой полуплоскости, чем вершина
С.
По
условию внутренние накрест лежащие
углы при параллельных прямых a, b и секущей
AB равны.
Из
равенства треугольников следует, что
∠
CAB = ∠
C1BA и ∠
CBA = ∠
C1AB и они совпадают с внутренними накрест
лежащими углами. Значит, прямая AC1
совпадает с прямой a, a прямая BC1 совпадает
c прямой b. Отсюда следует, что через две
различные точки С и С1 проходят две
различны прямые a и
b. Это противоречит аксиоме о том, что
«Через любые две точки можно провести
прямую, и только одну». Значит, прямые
параллельны.
Из
теоремы следует:
Две
прямые, перпендикулярные третьей,
параллельны.
На
основании теоремы доказывается:
Если
соответственные углы равны, то прямые
параллельны.
Если
сумма внутренних односторонних углов
равна 180°, то прямые параллельны.
Второй признак равенства треугольников
Теорема
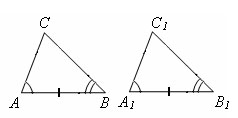 Если
сторона и прилежащие к ней углы одного
треугольника равны соответственно
стороне и прилежащим к ней углам другого
треугольника, то такие треугольники
равны.
Доказательство.
Пусть
у треугольников ABC и A1B1C1 ∠
A = ∠
A1, ∠
B = ∠
B1, AB = A1B1.
Если
сторона и прилежащие к ней углы одного
треугольника равны соответственно
стороне и прилежащим к ней углам другого
треугольника, то такие треугольники
равны.
Доказательство.
Пусть
у треугольников ABC и A1B1C1 ∠
A = ∠
A1, ∠
B = ∠
B1, AB = A1B1.
 Пусть
A1B2C2 – треугольник, равный треугольнику
ABC. Вершина B2 расположена на луче A1B1, а
вершина С2 в той же полуплоскости
относительно прямой A1B1, где лежит вершина
С1. Так как A1B2 = A1B1, то вершина B2 совпадает
с вершиной B1. Так как ∠
B1A1C2 = ∠
B1A1C1 и ∠
A1B1C2 = ∠
A1B1C1, то луч A1C2 совпадает с лучом A1C1, а
луч B1C2 совпадает с лучом B1C1. Отсюда
следует, что вершина С2 совпадает с
вершиной С1. Треугольник A1B1C1 совпадает
с треугольником A1B2C2, а значит, равен
треугольнику ABC. Теорема доказана.
Пусть
A1B2C2 – треугольник, равный треугольнику
ABC. Вершина B2 расположена на луче A1B1, а
вершина С2 в той же полуплоскости
относительно прямой A1B1, где лежит вершина
С1. Так как A1B2 = A1B1, то вершина B2 совпадает
с вершиной B1. Так как ∠
B1A1C2 = ∠
B1A1C1 и ∠
A1B1C2 = ∠
A1B1C1, то луч A1C2 совпадает с лучом A1C1, а
луч B1C2 совпадает с лучом B1C1. Отсюда
следует, что вершина С2 совпадает с
вершиной С1. Треугольник A1B1C1 совпадает
с треугольником A1B2C2, а значит, равен
треугольнику ABC. Теорема доказана.
|
|

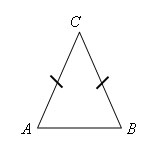 Треугольник
называется равнобедренным,
если у него две стороны равны. Эти
стороны называются боковыми (AC и
CB), а третья сторона называется
основанием (AB).
Треугольник
называется равнобедренным,
если у него две стороны равны. Эти
стороны называются боковыми (AC и
CB), а третья сторона называется
основанием (AB).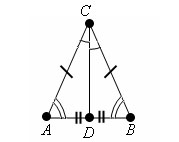 Доказательство.
Пусть
ABC – равнобедренный треугольник, а
CD медиана, проведенная к основанию
AB этого треугольника.
Треугольники
ACD и BCD равны по первому признаку
равенства треугольников, так как
AC=AB – так как ABC равнобедренный, AD=DB
– так как CD медиана и разбивает
основание AB пополам, ∠
CAD = ∠
CBD – так как ABC равнобедренный.
Из
равенства треугольников следует:
1)
так как ∠
ACD = ∠
BCD, то CD – биссектриса;
2)
так как ∠
CDA = ∠
CDB и эти углы смежные, то они по 90 ° и
CD – высота.
Теорема
доказана.
Доказательство.
Пусть
ABC – равнобедренный треугольник, а
CD медиана, проведенная к основанию
AB этого треугольника.
Треугольники
ACD и BCD равны по первому признаку
равенства треугольников, так как
AC=AB – так как ABC равнобедренный, AD=DB
– так как CD медиана и разбивает
основание AB пополам, ∠
CAD = ∠
CBD – так как ABC равнобедренный.
Из
равенства треугольников следует:
1)
так как ∠
ACD = ∠
BCD, то CD – биссектриса;
2)
так как ∠
CDA = ∠
CDB и эти углы смежные, то они по 90 ° и
CD – высота.
Теорема
доказана.