
Виды углов
 Два
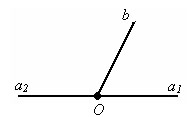
угла называются смежными, если у них
одна сторона общая, а другие стороны
являются дополнительными лучами. На
рисунке (a2b) и (a1b) смежные углы.
Теорема Сумма
смежных углов равна 180?.
Доказательство.
Пусть
∠(a2b)
и ∠(a1b)
– смежные углы. Полупрямая
b разбивает развернутый угол (a1a2) на два
угла. Значит ∠(a2b)
+ ∠(a1b)
= ∠
(a1a2) = 180?. Т.е. сумма смежных углов равна
180?. Теорема доказана.
Два
угла называются смежными, если у них
одна сторона общая, а другие стороны
являются дополнительными лучами. На
рисунке (a2b) и (a1b) смежные углы.
Теорема Сумма
смежных углов равна 180?.
Доказательство.
Пусть
∠(a2b)
и ∠(a1b)
– смежные углы. Полупрямая
b разбивает развернутый угол (a1a2) на два
угла. Значит ∠(a2b)
+ ∠(a1b)
= ∠
(a1a2) = 180?. Т.е. сумма смежных углов равна
180?. Теорема доказана.
 Теорема
Если
два угла равны, то смежные с ним углы
равны.
Доказательство.
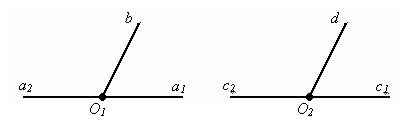
Углы
∠(a2b)
и ∠(a1b)
– смежные углы и ∠(с2d)
и ∠(с1d)
тоже смежные
углы.
Пусть
∠(a1b)
= ∠(с1d).
Но из ранее доказанного следует, что
∠(a1b)
+ ∠(a2b)
=180° и ∠(с1d)
+ ∠(с2d)
=180°. Тогда ∠(a1b)
=180° - ∠(a2b)
и ∠(с1d)
=180° - ∠(с2d).
А углы ∠(a1b)
и ∠(с1d)
равны, следовательно 180° - ∠(a2b)
=180° - ∠(с2d).
Из этого видно,
что ∠(a2b)
= ∠(с2d).
Теорема доказана.
Теорема
Если
два угла равны, то смежные с ним углы
равны.
Доказательство.
Углы
∠(a2b)
и ∠(a1b)
– смежные углы и ∠(с2d)
и ∠(с1d)
тоже смежные
углы.
Пусть
∠(a1b)
= ∠(с1d).
Но из ранее доказанного следует, что
∠(a1b)
+ ∠(a2b)
=180° и ∠(с1d)
+ ∠(с2d)
=180°. Тогда ∠(a1b)
=180° - ∠(a2b)
и ∠(с1d)
=180° - ∠(с2d).
А углы ∠(a1b)
и ∠(с1d)
равны, следовательно 180° - ∠(a2b)
=180° - ∠(с2d).
Из этого видно,
что ∠(a2b)
= ∠(с2d).
Теорема доказана.
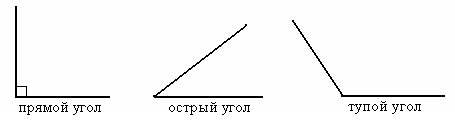 Угол
называется острым, если его градусная
мера которого больше 0°, но меньше
90°.
Угол
называется тупым, если его градусная
мера которого больше 90°, но меньше
180°.
Угол
равный 90°, называется прямым.
Если
угол острый, то смежный с ним угол тупой
и наоборот.
Угол
называется острым, если его градусная
мера которого больше 0°, но меньше
90°.
Угол
называется тупым, если его градусная
мера которого больше 90°, но меньше
180°.
Угол
равный 90°, называется прямым.
Если
угол острый, то смежный с ним угол тупой
и наоборот.
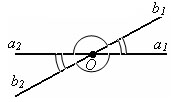
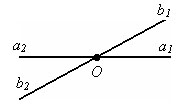 Два
угла называются вертикальными, если
стороны одного угла являются дополнительными
полупрямыми сторон другого угла. Пары
углов ∠(a2b2)
и ∠(a1b1),
∠(a2b1)
и ∠(a1b2)
– вертикальные углы.
Теорема.
Вертикальные
углы равны.
Доказательство.
Пусть
∠(a2b2)
и ∠(a1b1)
– вертикальные углы.
Угол (a2b1) является смежным ∠(a2b2)
и ∠(a1b1)
и дополняет их до 180°, по теореме о сумме
смежных углов, следовательно ∠(a2b2)
и ∠(a1b1)
равны. Теорема доказана.
Два
угла называются вертикальными, если
стороны одного угла являются дополнительными
полупрямыми сторон другого угла. Пары
углов ∠(a2b2)
и ∠(a1b1),
∠(a2b1)
и ∠(a1b2)
– вертикальные углы.
Теорема.
Вертикальные
углы равны.
Доказательство.
Пусть
∠(a2b2)
и ∠(a1b1)
– вертикальные углы.
Угол (a2b1) является смежным ∠(a2b2)
и ∠(a1b1)
и дополняет их до 180°, по теореме о сумме
смежных углов, следовательно ∠(a2b2)
и ∠(a1b1)
равны. Теорема доказана.
 ∠(a2b2)
= ∠(a1b1),
∠(a2b1)
= ∠(a1b2)
.
∠(a2b2)
= ∠(a1b1),
∠(a2b1)
= ∠(a1b2)
.
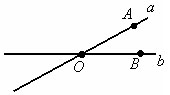 Углом
между прямыми a и b называется меньший
из углов с вершиной в точке O.
Углом
между прямыми a и b считается угол AOB.
Углом
между прямыми a и b называется меньший
из углов с вершиной в точке O.
Углом
между прямыми a и b считается угол AOB.
Угол
Углом
называется фигура, которая состоит из
точки (вершины угла) и двух лучей (стороны
угла), исходящих из этой точки.
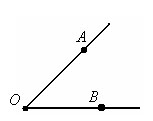 Угол
обозначается тремя точками «угол AOB»:
берется одна любая точка на одном из
лучей угла (точка А), вершина угла (точка
О) и одна любая точка на другом луче угла
(точка В). Можно обозначить это угол как
«угол ВОА». Запись «угол АОВ» и «угол
ВОА» обозначают один и тот же угол. В
место слова угол употребляют знак ∠.
Угол АОВ можно записать так:
1.
∠АОВ,
∠ВОА
;
2.
∠О
– точка О вершина угла;
3.
∠(ab)
– a и b лучи угла.
Угол
разбивает плоскость на две части. Каждая
часть называется плоским углом.
Дополнительными углами называются
плоские углы с общими сторонами.
Угол
обозначается тремя точками «угол AOB»:
берется одна любая точка на одном из
лучей угла (точка А), вершина угла (точка
О) и одна любая точка на другом луче угла
(точка В). Можно обозначить это угол как
«угол ВОА». Запись «угол АОВ» и «угол
ВОА» обозначают один и тот же угол. В
место слова угол употребляют знак ∠.
Угол АОВ можно записать так:
1.
∠АОВ,
∠ВОА
;
2.
∠О
– точка О вершина угла;
3.
∠(ab)
– a и b лучи угла.
Угол
разбивает плоскость на две части. Каждая
часть называется плоским углом.
Дополнительными углами называются
плоские углы с общими сторонами.
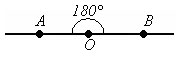
![]() Если
стороны угла являются дополнительными
полупрямыми одной прямой, то угол
называется развернутым. Угол СОD –
развернутый угол с вершиной О.
Если
стороны угла являются дополнительными
полупрямыми одной прямой, то угол
называется развернутым. Угол СОD –
развернутый угол с вершиной О.
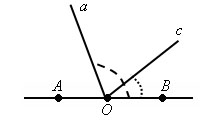
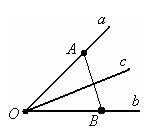 Говорят,
что луч проходит между сторонами данного
угла, если он исходит из его вершины и
пересекает какой-нибудь отрезок с
концами на сторонах угла. Луч с исходит
из точки О, проходит между сторонами
угла ab и пересекает отрезок
АВ.
Аксиома
Каждый
угол имеет определенную градусную меру,
большую нуля. Развернутый угол равен
180°. Градусная мера угла равна сумме
градусных мер углов, на которые он
разбивается любым лучом, проходящим
между его сторонами.
Углы
измеряются в градусах.
Говорят,
что луч проходит между сторонами данного
угла, если он исходит из его вершины и
пересекает какой-нибудь отрезок с
концами на сторонах угла. Луч с исходит
из точки О, проходит между сторонами
угла ab и пересекает отрезок
АВ.
Аксиома
Каждый
угол имеет определенную градусную меру,
большую нуля. Развернутый угол равен
180°. Градусная мера угла равна сумме
градусных мер углов, на которые он
разбивается любым лучом, проходящим
между его сторонами.
Углы
измеряются в градусах.
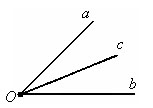 Угол
(ab) равен сумме углов (ac) и (cb). ∠(ab)
= ∠(ac)
+ ∠(cb).
Аксиома
От
любого луча в заданную полуплоскость
можно отложить угол с заданной градусной
мерой, меньшей 180°, и только один.
Угол
(ab) равен сумме углов (ac) и (cb). ∠(ab)
= ∠(ac)
+ ∠(cb).
Аксиома
От
любого луча в заданную полуплоскость
можно отложить угол с заданной градусной
мерой, меньшей 180°, и только один.
Угол
Углом называется фигура, которая состоит из точки (вершины угла) и двух лучей (стороны угла), исходящих из этой точки. Угол обозначается тремя точками «угол AOB»: берется одна любая точка на одном из лучей угла (точка А), вершина угла (точка О) и одна любая точка на другом луче угла (точка В). Можно обозначить это угол как «угол ВОА». Запись «угол АОВ» и «угол ВОА» обозначают один и тот же угол. В место слова угол употребляют знак ∠. Угол АОВ можно записать так: 1. ∠АОВ, ∠ВОА ; 2. ∠О – точка О вершина угла; 3. ∠(ab) – a и b лучи угла. Угол разбивает плоскость на две части. Каждая часть называется плоским углом. Дополнительными углами называются плоские углы с общими сторонами. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым. Угол СОD – развернутый угол с вершиной О. Говорят, что луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла. Луч с исходит из точки О, проходит между сторонами угла ab и пересекает отрезок АВ. Аксиома Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами. Углы измеряются в градусах. Угол (ab) равен сумме углов (ac) и (cb). ∠(ab) = ∠(ac) + ∠(cb). Аксиома От любого луча в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
