19.Алгоритм симплексного метода
Приведем для этого введем допол-е неотриц переменные:
Которые обратят каждое неравенство в равенство и эти дополнительные переменные в целевую функцию не входят.
(1’)
(3’)
(2’) в векторном виде
На основании того,что векторы (**)линейно независимы исходный опорный план имеет вид:
Базис |
|
|
|
… |
|
… |
|
|
|
… |
|
… |
|
|
|
|
|
… |
|
… |
|
1 |
0 |
… |
0 |
… |
0 |
|
|
|
|
… |
|
… |
|
0 |
1 |
… |
0 |
… |
0 |
… |
… |
…. |
…. |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
… |
|
… |
|
0 |
0 |
… |
1 |
… |
0 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
… |
|
… |
|
0 |
0 |
… |
0 |
… |
1 |
|
0 |
|
|
… |
|
… |
|
0 |
0 |
… |
0 |
… |
0 |
Шаг1. Проверка плана на оптимальность
Если в последней строке табл.
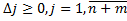,то
в соответствии критериями опимальности
плана ненулевые компоненты которого
расположены в столбцах p0
оптимальны
Если же
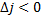,для
некоторых фиксированных j,то
план Хнеоптимален возможно либо его
улучшение, либо определится ,что задача
неразрешима
Шаг2. Определение вектора вводимого в базис.
min
k
--это
означает,что вектор Pk
вводится в базис,а
столбец k
ведущий.
Шаг 3.Определение вектора выводимого из базиса .
Для
этого определяет величину 
выводим
из базиса
Замечание .
Если
aik
<0,где
i=1,
то
задача не имеет решения.
Шаг 4. Преобразование таблицы по формулам Жордана-Гаусса
1)элементы ведущей строки определяются делением всех элементов этой строки на ведущий элeмент.
2)Элементы ведущего столбца равны 0за исключением ведущего, j равен единице.
Остальные
элементы определяются по формуле: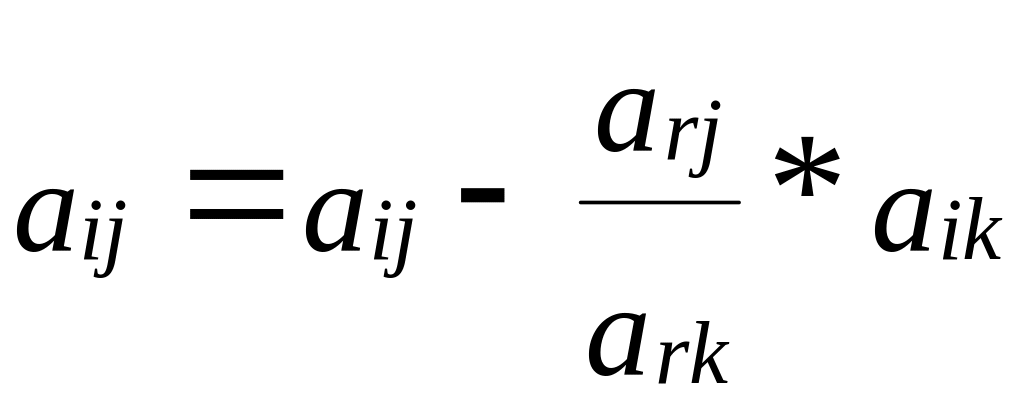
Эти переменные опред по правилу прямоугольника
в результате этих преобразований будетполучена новая таблица,новый опорный план и с большими значениями целевой функции переходим к шагу 1 данный процесс продолжается до тех пор пока не будет получен оптимальный план,либо будет определено что задача не разрешима.