9) Основная теорема двойственности

1)Если одна из двойственных задач имеет решение, то и 2 задача разрешима, при чем экстремальные значения линейных форм обеих задач совпадают, т.е. maxf(x)=maxg(y) 2)Если же одна из задач неразрешима, то другая задача не имеет ни одного плана.

10) Постановка и математическая модель транспортной задачи Постановка задачи

В m пунктах отправления А1,А2,…,Аm имеется однородный груз в количествах а1,а2,…,аm. Этот груз необходимо отправить в n пункты потребления В1,В2,…,Вn,спрос, которого составляет b1,b1,…,bn. Задано: Сij-транспортные затраты на перевозку единицы груза и из пункта Аi в пункт Вj (i=1,m; j=1,n). Определить такой план перевозок при котором весь груз из пунктов отправления будет выведен, спрос всех потребителей удовлетворен и при этом суммарные транспортные задачи будут минимальными. Матем.модель. Введем переменные: Хij- объем груза из Аi→ Вj (i=1,m; j=1,n).

X= 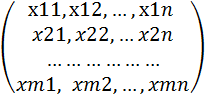план перевозок

Всю данную информацию поместим в распределительную таблицу:

Ai/Bj	B1	B2	…	Bn
A1	C11 x11	C12 x12	…	C1n x1n
A2	C21 x21	C22 x22	…	C2n x2n
…	…	…	…	…
An	Cm1 xm1	Cm2 xm2		Cmn xmn

Целевая функция:

1. L(x)=C₁₁X₁₁+C₁₂X₁₂+…+C_1nX_1n+C₂₁X₂₁+C₂₂X₂₂+...+ +C_2nX_2n+….+C_m1X_m1+ +C_m2X_m2+...+C_mnX_mn→min

_{m n}

L(x)=∑∑CijXij→min ^{i=1 j=1} _n

Ограничение 1: ∑Xij=ai, i=1,m x₁₁+x₁₂+..+x_1n=a₁ (←eto sistema) (2) ^j=1 x₂₁+x₂₁+..+x_2n=a₂ …………………….

x_m1+x_m2+..+x_mn=a_n

Условие, что все поставщики должны быть полностью разгружены Ограничение 2 _m x₁₁+x₁₂+..+x_m1=b₁ (←eto sistema) (3) ∑Xij=bj, j=1,n x₂₁+x₂₁+..+x_m2=b₂ ⁱ⁼¹ …………………….

x_1n+x_2n+..+x_mn=b_n

Условие,что спрос всех потребителей удовлетворен Ограничение 3: (4) Xij≥0 i=1,m j=1,n Перевозки только в одном направлении (из Ai→Bj) (i=1,m; j=1,n).

Ограничения (2) и (3) в векторном виде:

(5) P₁₁X₁₁+P₁₂X₁₂+...+P_1nX_1n+P₂₁X₂₁+P₂₂X₂₂+…+P_2nX_2n+…+P_m1X_m1+P_m2X_m2+…+P_mnX_mn=P₀ Определение1: Всякое неотрицательное реш-е системы (2)и(3), определяемое матрицей X=//Xij//m*n наз-ся планом транспортной задачи Определение2: План X=//Xij//m*n называется опорным, если векторы Рij входящие в разложение (5) с ненулевыми коэффициентами линейно-независимо. Определение3: Опорный план X=//Xij//m*nназывается невырожденным, если он содержит ровно m+n-1 ненулевых элементов. Определение4: План X=//Xij//m*n, при котором целевая функция достиг мин. значения называется оптимальным.