1.Этапы процесса моделирования экономических задач
В основе экономико-математ. исследования лежит математ. моделирование изучаемого эконом. процесса, т.е. описание количественных закономерностей этого процесса с помощью математ. выражении.
Моделирование-процесс построения, изучения и применения моделей.
1-Этап. Построение модели. При построении модели приходится решать три задачи:
1) Определение цели исследования;
Определение показателя по которому будут сравниваться и выбираться наилучшие решения. Напр: минимум затрат, максимум прибыли
2) Выявление основных ограничений;
Необходимо выявить ресурсы, которые существенно влияют на результат и отбросить несущественные.
3) Количественное выражение исходных данных. Только в случае, когда можно найти количественное выражение, только тогда можно составить экономическую модель
Построение модели начинается с введения переменных, количественное выражение которых определяет один из вариантов решения. Затем используем введенные переменные и количественное выражение исходных данных и составляется целевая функция и ограничения задачи. В самом общем виде математическая модель экономической задачи имеет вид:
f(х1,
х2,
…, хn)
→
еxtr(max,
min)
при условиях gi
(x1,
x2,
…, xn)
≤ bi,
xj
≥0,
2-Этап. Изучение модели. Производятся модельные эксперименты
3-Этап. Перенос знаний с модели на объект. Тут осуществляется переход от языка объекта на реальный язык. Если при этом модель недостаточно реально отражает изучаемый объект исследования, то осуществляется переход к этапу-1, производится корректировка модели, т е моделирование- это циклический процесс, который продолжается до тех пор пока не будет получена модель достаточно адекватно отражающий объект.
2.Задачи этапа построения модели
Моделирование-процесс построения, изучения и применения моделей.
Моделирование состоит из 3 этапов: построение модели;
изучение модели; перенос знаний с модели на объект
При построении модели приходится решать три задачи:
1) Определение цели исследования;
Определение показателя по которому будут сравниваться и выбираться наилучшие решения. Напр: минимум затрат, максимум прибыли
2) Выявление основных ограничений;
Необходимо выявить ресурсы, которые существенно влияют на результат и отбросить несущественные.
3) Количественное выражение исходных данных. Только в случае, когда можно найти количественное выражение, только тогда можно составить экономическую модель
Построение модели начинается с введения переменных, количественное выражение которых определяет один из вариантов решения. Затем используем введенные переменные и количественное выражение исходных данных и составляется целевая функция и ограничения задачи. В самом общем виде математическая модель экономической задачи имеет вид:
f(х1, х2, …, хn) → еxtr(max, min) при условиях gi (x1, x2, …, xn) ≤ bi,
xj ≥0,
3.Различные формы задачи линейного программирования
1.Общая задача линейного программирования (ЛП)
Найти max f(х)=c1х1 + c2х2 + …+ cnхn при ограничениях:
2.Стандартная форма задачи ЛП
Найти max f(х)=c1х1 + c2х2 + …+ cnхn при ограничениях:
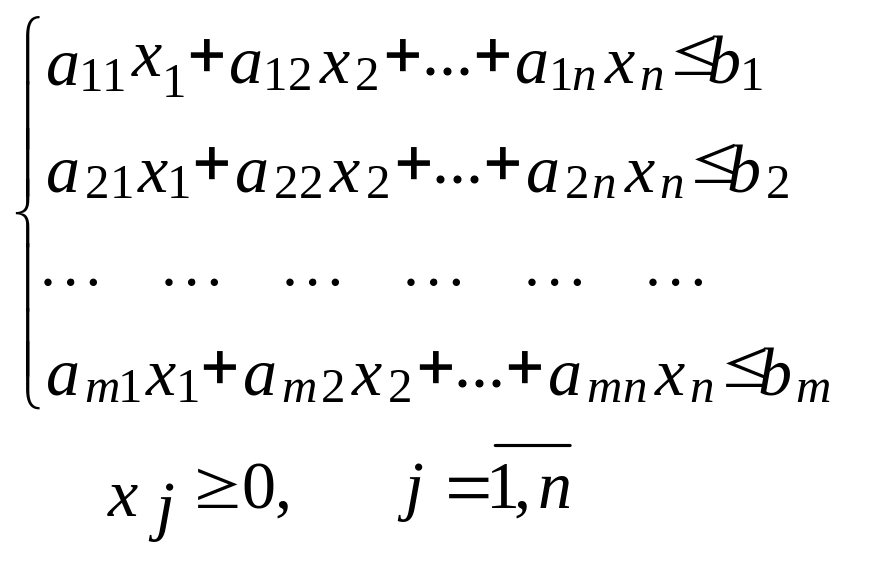
3. Каноническая форма задачи ЛП:
Найти max f(х)=c1х1 + c2х2 + …+ cnхn при условиях:
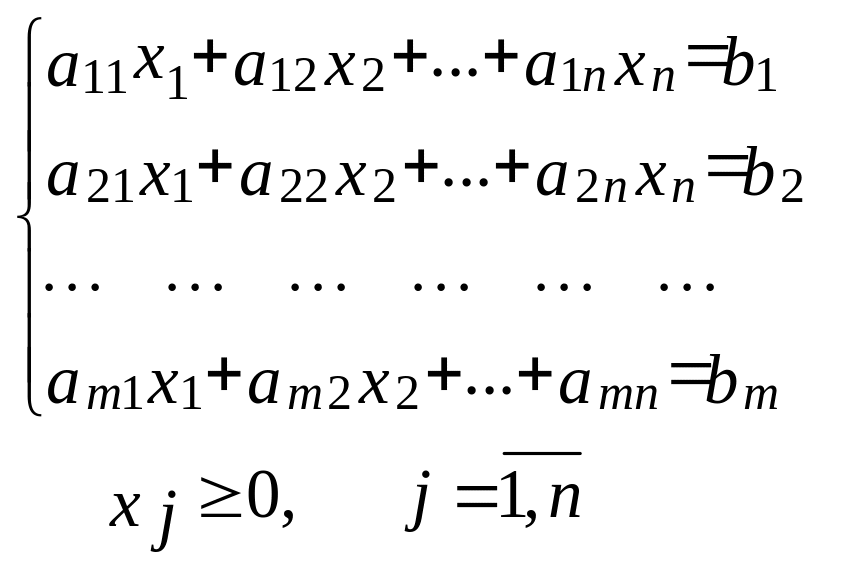
Векторная запись канонической формы ЗЛП
max f(х)=c1х1 + c2х2 + …+ cnхn
p 1x1+ p2x2+….+pnxn=p0
x j ≥0, j=1,n
(a11) (a21) ( a1n) ( b1)
p1= (a21) , p2= (a22) , ….. , pn= (a2n ) p0= ( b2)
…. …. …. .…
(am1) (am2) (amn) (bm)