Игры с природой (статистические игры)

Статистические игры образуют специальный класс матричных игр, в которых одним из участников является человек или группа лиц, объединенных общей целью – т.н. статистик (игрок А), другой участник – природа (игрок П). «Природа» - комплекс внешних условий, при которых статистику приходится принимать решение. Любую хозяйственную деятельность человека можно рассматривать как игру с природой. Природа безразлична к выигрышу.

Пусть статистик имеет m стратегий ; природа может реализовать n различных состояний .

Такие игры, в основном бывают 2-х типов: когда известны вероятности реализации состояний природы 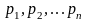и когда неизвестны.

Если статистик может численно оценить применение каждой своей стратегии при любом состоянии природы , то игру можно задать платежной матрицей:

	П1	П2	…	Пn
A1	a11	a12	…	a1n
A2	a21	a22	…	a2n
…	…
Am	am1	am2	…	amn
pj	P1	P2	…	Pn

При упрощении платежной матрицы нельзя отбрасывать те или иные состояния природы, т.к. природа может реализовать любое из своих состояний независимо от того, выгодно это статистику или нет. Природа может даже помогать игроку А.

При выборе оптимальной стратегии статистика пользуются различными критериями, ни один из которых не является универсальным. Поэтому следует по очереди применять все эти критерии. Если одна из стратегий игрока фигурирует в качестве лучшей чаще других, то она в результате принимается оптимальной.

При решении опираются как на платежную матрицу, так и на матрицу рисков.

Риском статистика 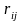при использовании им стратегии при состоянии природы называется разность между максимальным выигрышем, который он мог бы получить. Если бы достоверно знал, что природой будет реализовано состояние и тем выигрышем, который он получит, не зная какое же состояние природа реализует. Т.е. . ( ).

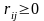Матрица рисков имеет ту же размерность, что и платежная матрица:

И формируется по столбцам: в каждом столбце платежной матрицы выбирается наибольший элемент, который в матрице рисков заменяют нулем, а остальные элементы столбца матрицы рисков получают вычитанием соответствующих элементов из этого наибольшего элемента.

Рассмотрим критерии, которые применяются для определения оптимальной стратегии.

1-й случай. Вероятности состояний природы неизвестны:

1. Критерий максимума математического ожидания выигрыша.

Критерий Лапласа: все состояния считаются равновероятными:

Тогда средний выигрыш по каждой стратегии рассчитывается как среднее арифметическое выигрышей по всем возможным состояниям природы: .

В качестве оптимальной выбирается стратегия, которая обеспечивает максимальную величину среднего выигрыша статистика, т.е. .

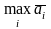2. Критерий наименьшего среднего риска заключатся в подборе стратегии, обеспечивающей наименьший средний риск статистика: .

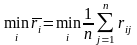3. Максиминный критерий Вальда: Оптимальной считается стратегия А_i, при которой наименьший выигрыш статистика будет максимальным.

Это пессимистический критерий. В матрице выигрышей (т.е. платежной матрице) в каждой строке выбирается наименьший элемент, а затем среди этих элементов выбирается наибольший: .

4. Критерий Сэвиджа: оптимальной считается стратегия, которая минимизирует величину максимального риска, т.е. из каждой строки матрицы рисков выбирается максимальный элемент, а затем среди этих элементов выбирается строка, в которой находится минимальный элемент:

5. Критерий пессимизма-оптимизма Гурвица: Оптимальной считается стратегия, найденная из условия: ,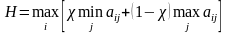

гд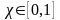е - «коэффициент пессимизма-оптимизма». При χ = 1 имеем критерий Вальда, или критерий крайнего пессимизма, при χ = 0 – критерий «крайнего оптимизма». Рекомендуется выбирать χ между нулем и единицей, из субъективных соображений. (Чем сложнее ситуация, тем ближе χ к единице).