49 Частотное управление ад при постоянном потокосцеплении статора. Структура системы управления.

Частотное управление АД не сопряжено с конструкцией электродвигателя или введением в него дополнительных элементов. Сложность при управлении – это зависимость момента от двух активных изображающих векторов, т.е. от четырех взаимосвязанных параметров. Для упрощения используются приемы, при которых момент является функцией одной величины. При частотном управлении используются два метода однозначности момента: при постоянстве потокосцепления статора ₁ и при постоянстве потокосцепления ротора ₂.

Система с постоянным потокосцеплением статора.

Для рассмотрения данного вопроса воспользуемся обобщенной машиной:

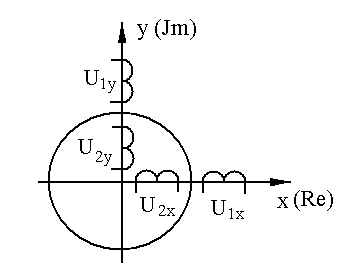Имеем исходное уравнение для обобщенной машины

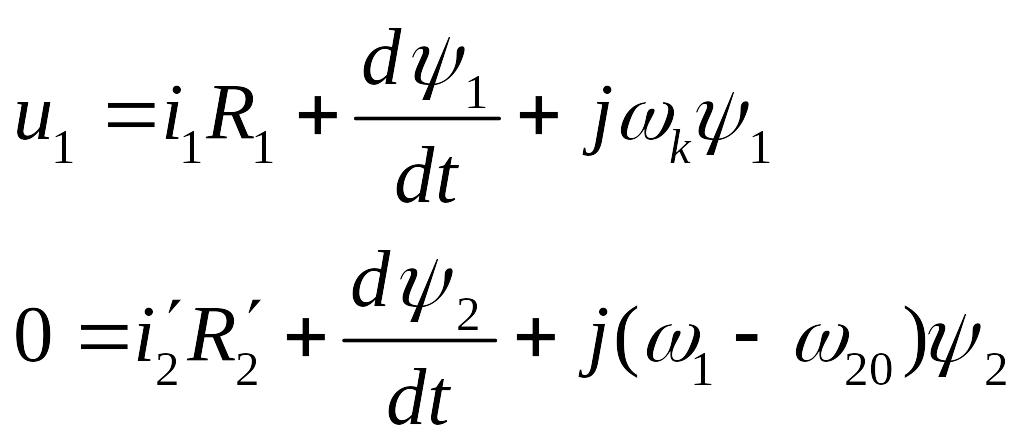
_к – произвольная скорость вращения координат. В нашем случае _к=₀,

₂₀ – скорость вращения ротора для двухполюсного двигателя.

В нашем случае имеем систему:

Рассмотрим случай, когда R₁=0. Принимаем ₁=Const. . Кроме того, напряжение u₁ совмещаем с ось х. , тогда из первого уравнения системы имеем , т.о. .

Из выражения для момента выбираем

Имеем , но следовательно , т.е. имеем ; Z_p – число пар полюсов. Т.е. получили , осуществлен переход к амплитудным значениям напряжения и тока.

Определим из схемы замещения.

Р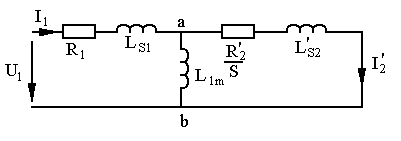 ассмотрим при R₁=0. В схеме замещения будет использоваться индуктивность , . Воспользуемся методом эквивалентного генератора относительно зажимов ab.

;

.

.

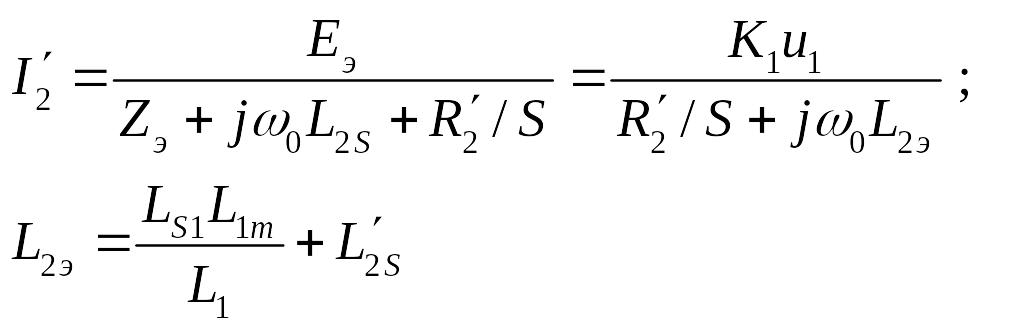Следовательно, имеем

;

;

S_M – критическое скольжение.

Т.о. получим выражение для момента .

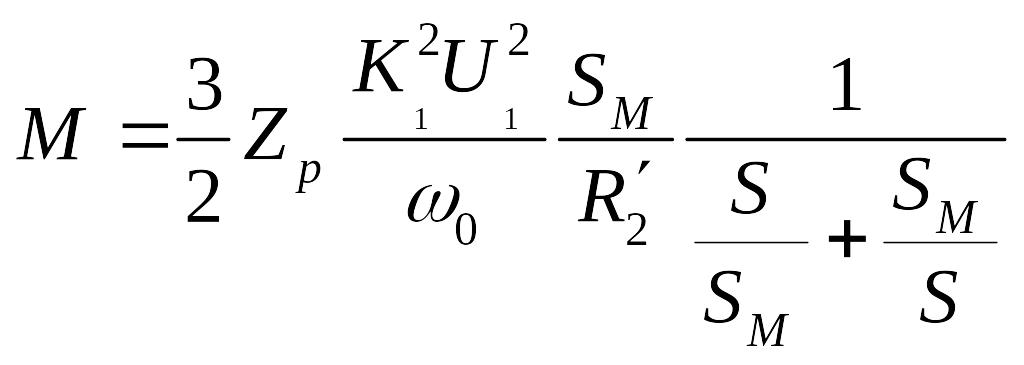Определим статическую характеристику электродвигателя при S<<S_M, как частный случай. Тогда имеем:

при постоянстве ₁: .

П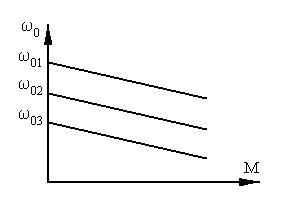 ри частотном управлении изменяется ₀ и u₁, так, чтобы ₁ было постоянным, т.е. тогда имеем выражение для момента , где К_ДМ=Const – коэффициент наклона характеристики.

Следовательно, имеем выражение характеристики для рабочего участка: .

Рассмотрим элементы динамики. В цепи статора потокосцепление постоянное, следовательно на динамику влияет потокосцепление ротора, т.е. рассматривается выражение: . Из имеющихся соотношений:

Из этой системы можно получить, что .

Имеем далее .

После преобразования имеем , где .

Т.к. S<<S_M, то пренебрегаем, тогда имеем .

Т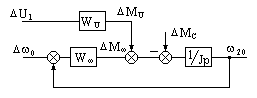 .о. имеем зависимость момента от угловой скорости .

Представление об управлении будет не полным, если не учитывать влияние на изменение момента, изменения напряжения U₁. Обычно передаточная функция по напряжению либо рассчитывается приближенно, либо определяется экспериментально. Если подойти классически, то приращение момента следует рассматривать как функцию от приращения двух переменных S и  U₁, т.е. имеем ;

П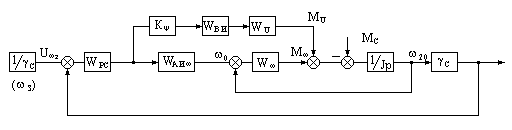 олучаем соответствующую передаточную функцию

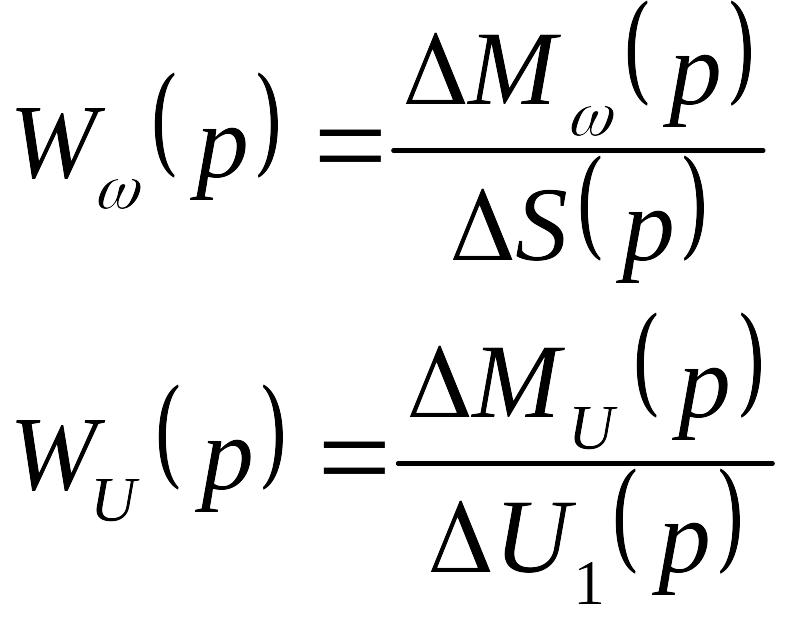
Если рассматривать по приращению, то при определении W_ в статике имеем постоянную ; а из уравнения для цепи ротора ; . Когда получим выражение для W_(p) следует перейти к абсолютному скольжению .

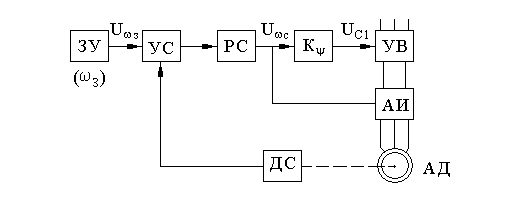- функция двух переменных, следовательно

При определении передаточной функции W_U(p) постоянной принимается только скольжение, следовательно остальные параметры переменны. Следовательно из уравнения для статора имеем (при R₁=0). Из уравнения для ротора имеем ; .

Для полученных передаточных функций, присовокупив , имеем структуру:

Следует учитывать, что был рассмотрен случай при R₁=0 в реальности эта соотношение не соблюдается, поэтому зависимость задаваемого напряжения от частоты нелинейная. При R₁=0 . Сказывается падение напряжения на R₁ особенно на частотах ₀<<_0н (_0н – нелинейная паспортная частота). . Т.о. коэффициент передачи вобщем нелинейная величина. Зависимость имеет вид:

Ф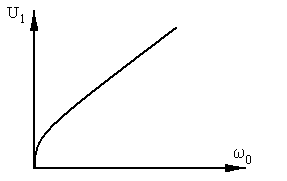 ункциональная схема наиболее простой, но распространенной системы имеет вид:

ЗУ – задающее устройство;

УС – устройство сравнения;

РС – регулятор скорости;

ДС – датчик скорости;

УВ – управляемый выпрямитель;

АИ – автономный инвертор;

К_ - функциональный преобразователь.

Структура системы: