Контрольні завдання
Тема 1. Похідна і диференціал функції. Похідні вищіх порядків.
Застосовування похідної та диференціалу. Література: [2, р. 2, 3], [7, р. 5, 6]
1-10. Знайти похідні першого порядку та диференціали функцій:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11-20. Знайти похідні другого порядку
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21-30. Дослідити функції та побудувати їх графіки.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Тема 2. Диференціальне числення функції багатьох змінних.
Література: [2, р.4], [7, р.9]
31-40. Знайти максимальну абсолютну та відносну похибки функції:
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41-50. Знайти екстренум функції двох змінних:
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
Тема 3. Інтегральне числення та його застосування.
51-70. Знайти інтеграли:
51.
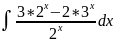
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71-80. Обчислити визначений інтеграл:
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81-90. Знайти середнє значення функції на інтервалі [a,b]:
81.
82.
83.
84.
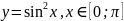
85.
86.
87.
88.
89.
90.
91-100. Обчислити площу, обмежену лініями:
91.
92.
93.
94.
95. y=ln x, x=0, y=ln a, y=ln b
96.
97.
98.
99.
100.
Тема 4. Диференціальні рівняння.
101-110. Знайти загальний розв’язок диференціального рівняння.
101.
102. x y (1+x^2)y’=1+y^2
103.
104.
105.
106.
107.
108.
109.
110.
111-120. Знайти частковий розв’язок диференціального рівняння при початкових умовах y(x0)=y0:
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121-130. Знайти загальний розв’язок диференціального рівняння:
121.
122.
123.
124.
125.
126.
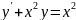
127.
128.
129.
130.
131-140. Знайти частковий розв’язок лінійного однорідного диференціального рівняння другого порядку зі сталими коефіцієнтами при початкових умовах у(0)=у0; y’(0)=y’0
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
Тема 5. Основні поняття теорії ймовірностей.
141. В урні маємо 10 куль: 3 білих і 7 чорних. З урни наугад вибирають 2 кулі. Яка ймовірність того, що ці кулі: а) обидві білі; б) обидві чорні; в) різного кольору; г) одного кольору.
142. З п’яти карток з літерами А, Б, В, Г, Д наугад одна за одною вибирають три і розташовують в ряд у порядку з’явлення. Яка ймовірність того, що утвориться слово «ДВА»?
143. Ймовірність того, що на протязі однієї зміни виникає неполадка верстату, дорівнює 0.05. Яка ймовірність того, що не відбудеться ні одної неполадки за три зміни?
144. Студент прийшов на залік, знаючи з 30 питань тільки 24. Яка ймовірність здачі заліку, якщо після відмови відповідати на питання викладач задає ще одне питання?
145. Спостереженням встановлено, що в деякій місцевості у вересні в середньому буває 12 дощових днів. Яка ймовірність, що з випадково взятих в цьому місяці 8 днів 3 дні будуть дощовими?
146. Ймовірність отримання вдалого результату при проведенні складного хімічного досліду має 2/3. Найти ймовірність п’яти вдалих результатів в 7 дослідах.
147. Ймовірність народження хлопчика дорівнює 0,515, дівчинки – 0,485. В деякій сім’ї шестеро дітей. Знайти ймовірність того, що серед них не більше двох дівчинок.
148. Що ймовірніше: виграти у рівносильного супротивника (виключаючи ничію) три партії з п’яти, або п’ять з восьми?
149. З партії в 25 виробів, серед яких 6 бракованих, вібрані випадковим чином 3 вироби для перевірки їх якості. Знайти ймовірність того, що: а) всі вироби годні; б) серед виробів 1 бракований; в) всі вироби браковані.
150. Що ймовірніше: вгадати 6 номерів в спортивній лотереї 6 з 45, або 5 номерів в Спортлото – 5 з 36?