Замена переменной в определенном интеграле
Определенный интеграл
по
переменной x можно преобразовать в
определенный интеграл относительно
переменной t с помощью подстановки
x = g (t):
Новые пределы интегрирования по переменной t определяются выражениями
где g -1 - обратная функция к g, т.е. t = g -1(x).
Интегрирование по частям для определенного интеграла
В этом случае формула интегрирования по частям имеет вид:
где
означает
разность значений произведения функций
uv при x = b и x = a.
Пример 1
Вычислить интеграл
.
Решение.
Применяя формулу Ньютона-Лейбница, получаем
Пример 2
Вычислить интеграл
.
Решение.
Пример 3
Вычислить интеграл
.
Решение.
Сделаем замену:
Пересчитаем пределы интегрирования. Если x = 0, то t = −1. Если же x = 1, то t = 2. Тогда интеграл через новую переменную t легко вычисляется:
Пример 4
Вычислить интеграл
.
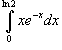Решение.
Запишем интеграл в виде
Используем
интегрирование по частям:
.
В нашем случае пусть будет
Следовательно, интеграл равен
Пример 5
Найти площадь фигуры,
ограниченной кривыми
и
.
Решение.
Сначала определим точки пересечения двух кривых (рисунок 3).
Таким образом, данные кривые пересекаются в точках (0,0) и (1,1). Следовательно, площадь фигуры равна
|
|
|
Рис.3 |
|
Рис.4
|
Пример 6
Найти площадь фигуры,
ограниченную графиками функций
и
.
Решение.
Найдем координаты точек пересечения кривых (рисунок 4).
Данная область
ограничивается сверху параболой
,
а снизу - прямой линией
.
Следовательно, площадь этой области
равна
