Подготовила: Киселева И.В.

Первообразная функции, ее свойства. Неопределенный интеграл. Простейшее интегрирование функций

Определение 1. Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной для F(x), т.е. .

Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования: по заданной функции f(x ) требуется найти функцию F(x), производная которой равна f(x).

Первообразная определена неоднозначно: для функции первообразными будут и функция arctg x, и функция arctg x-10: .

Свойства первообразной

1. Если функция F(x) - первообразная для функции f(x) на интервале X, то функция f(x) + C, где C - произвольная постоянная, тоже будет первообразной для f(x) на этом интервале.

2. Если функция F(x) - некоторая первообразная для функции f(x) на интервале X=(a,b), то любая другая первообразная F₁(x) может быть представлена в виде F₁(x) = F(x) + C, где C - постоянная на X функция.

3. Для любой первообразной F(x) выполняется равенство dF(x) = f(x) dx.

Из этих свойств следует, что если F(x) - некоторая первообразная функции f(x) на интервале X, то всё множество первообразных функции f(x) (т.е. функций, имеющих производную f(x) и дифференциал f(x) dx) на этом интервале описывается выражением F(x) + C, где C - произвольная постоянная.

Неопределённый интеграл и его свойства

Определение 2. Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом .

Если F(x) - некоторая первообразная функции f(x), то , где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.

Свойства неопределённого интеграла, непосредственно следующие из определения:

1. .

2. (или ).

Таблица неопределённых интегралов

1	.
2	.
3	( ).
4	.
5	; .
6	.
7	.
8	.
9	.
10	.
11	.
12	.
13	.
14	.
15	.
16
17	.
18	.
19	.
20	; .

Любая непрерывная функция имеет первообразную и, как следствие, неопределённый интеграл. При изучении дифференцирования было установлено, что с помощью таблицы производных и правил дифференцирования без труда можно получить производную любой элементарной функции, и эта производная тоже будет элементарной функцией. Операция интегрирования этим свойством не обладает: даже относительно простые функции могут иметь первообразные, которые через элементарные функции не выражаются.

Доказано, что не берутся в элементарных функциях следующие интегралы, относящиеся к классу специальных функций:

- интеграл Пуассона;

, - интегралы Френеля;

, , - интегральные синус, косинус, логарифм.

Простейшие правила интегрирования

1. ( );

2. ;

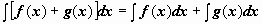Пример 1

Пример 2.

3. Подведение под знак дифференциала постоянного слагаемого: если , то .

Пример 3

.

3. Подведение под знак дифференциала постоянного множителя: если , то .

Пример 4

.

Приёмы 3, 4 легко комбинируются: если , то:

.

Пример 5

.

Замена переменной в неопределённом интеграле

(интегрирование подстановкой) и интегрирование по частям.

Интегрирование подстановкой

Пусть . Тогда . Здесь t(x) - дифференцируемая монотонная функция.

При решении задач замену переменной можно выполнить двумя способами.

1. Если в подынтегральной функции удаётся сразу заметить оба сомножителя, и f(t(x)), и , то замена переменной осуществляется подведением множителя под знак дифференциала: , и задача сводится к вычислению интеграла .

Пример 1

(задача сведена к вычислению , где t = cos x) (аналогично находится интеграл от ); (задача сведена к вычислению , где t = sin x) .

2. Замену переменной можно осуществлять формальным сведением подынтегрального выражения к новой переменной. Так, в имеет смысл перейти к переменной (сделать подстановку) t = sin x.

Выражаем все множители подынтегрального выражения через переменную t:

; в результате

(возвращаемся к исходной переменной) .

Другие примеры:

. Подынтегральная функция содержит два множителя, ни один из которых не является производной другого, поэтому подводить их под знак дифференциала бесполезно. Попытаемся ввести новую переменную, такую, чтобы корни извлеклись:

= .

Рассмотрим (интеграл №19 из табл. неопределённых интегралов). Здесь подынтегральная функция состоит из единственного множителя; можно опять попытаться сделать такую замену переменной, чтобы корень извлёкся. Структура подкоренного выражения подсказывает эту замену: (или , ): .

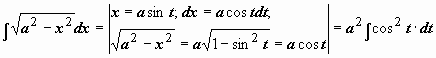Интеграл свёлся к интегралу от квадрата косинуса. При интегрировании чётных степеней синуса и косинуса часто применяются формулы, выражающие и через косинус двойного угла:

.

Поэтому

.

Искусство интегрирования в основном заключается в умении видеть необходимые подстановки; оно, как и любое другое искусство, вырабатывается упражнениями. Для основных классов функций требуемые подстановки будут изучаться дальше, здесь мы покажем, с помощью каких преобразований были выведены формулы 17, 15, 20 Таблицы неопределённых интегралов:

.

.

.

Второй интеграл элементарно сводится к первому:

.