
- •Основы кинематики
- •7. Элементы механики жидкостей
- •13 . Первое и второе и третье начало термодинамики
- •19. Магнитное поле
- •25. Идеальный и реальный колебательные контуры
- •3.4.2.Свободные колебания в реальном контуре
- •Фотоэлектрический эффект, законы внешнего фотоэффекта, уравнение Эйнштейна
- •7. Экспериментальное исследование дифракции света
- •13. Определение ускорения свободного падения с помощью математического маятника
Основы кинематики




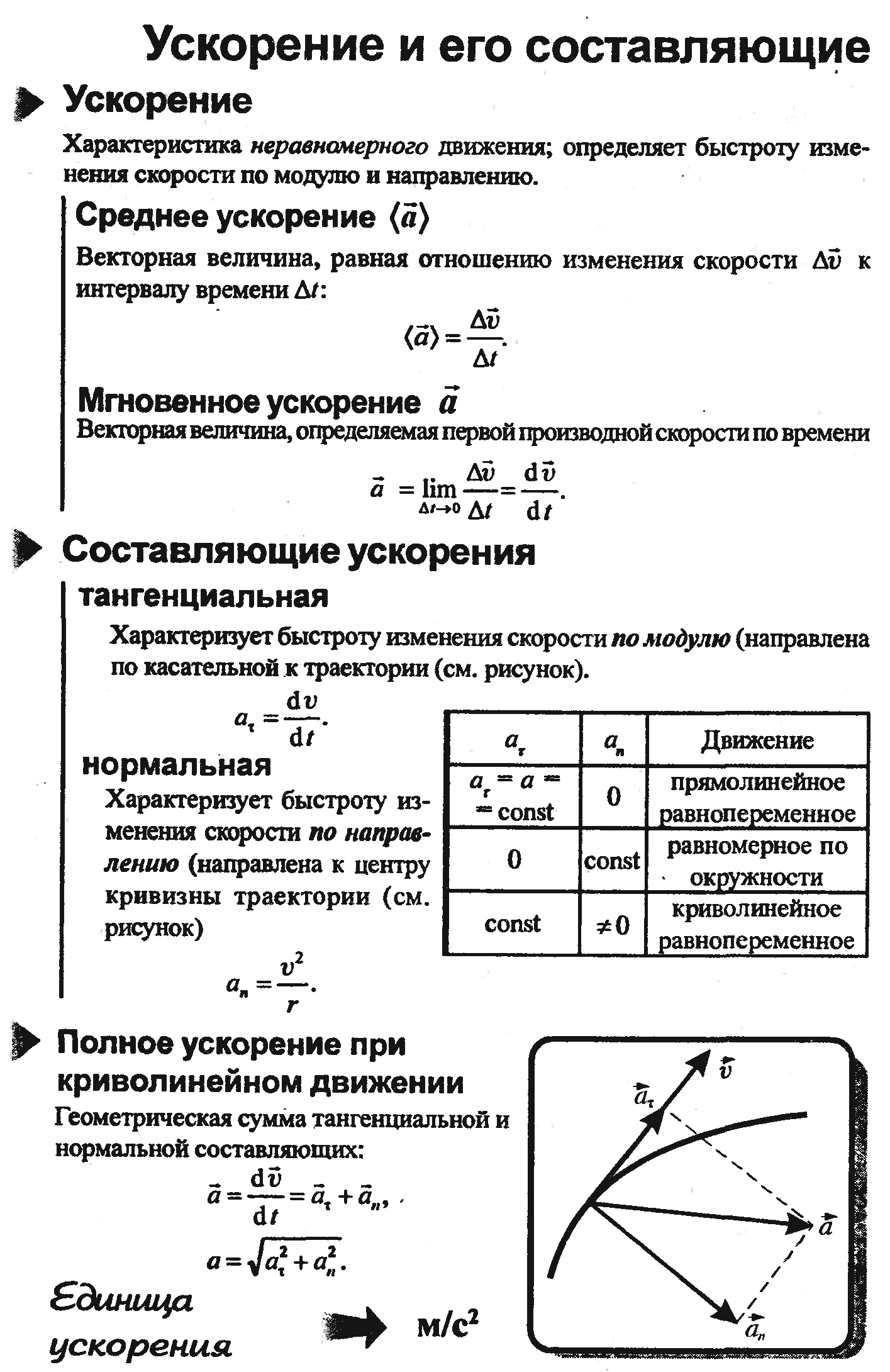


7. Элементы механики жидкостей





13 . Первое и второе и третье начало термодинамики

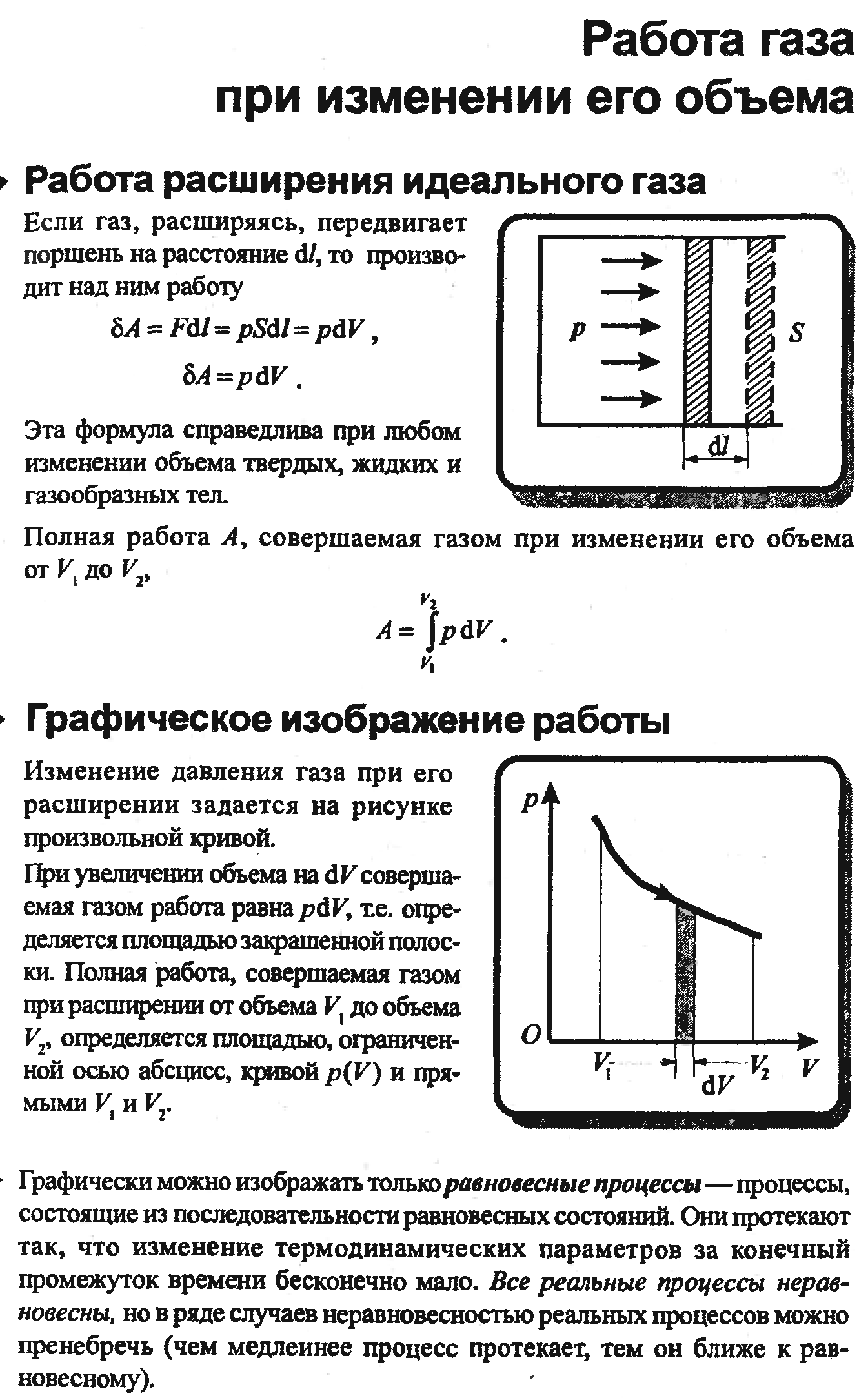


1. Первый и второй законы термодинамики не позволяют определить значение S0 энтропии системы при абсолютном нуле температуры (T = 0°К). В связи с этим оказывается невозможным теоретический расчет абсолютных значений энтропии,изохорно-изотермного и изобарно-изотермного потенциалов системы, а также константы равновесия. 2. На основании обобщения экспериментальных исследований свойств различных веществ при сверхнизких температурах был установлен закон, устранивший указанную трудность и получивший название принципа Нернста или третьего закона термодинамики. В формулировке Нернста он гласит: в любом изотермическом процессе, проведенном при абсолютном нуле температуры, изменение энтропии системы равно нулю, т. е. DS (T=0) = 0, S = S0 = const, независимо от изменения любых других параметров состояния (например, объема, давления, напряженности внешнего силового поля и т. д.). Иными словами, при абсолютном нуле температуры изотермический процесс является также и изоэнтропийным. 3. Из третьего закона термодинамики следует, что для всех тел при T = 0°К обращаются в нуль теплоемкости Сp и СV и термодинамический коэффициент расширяемости a. Из него также вытекает вывод о невозможности осуществления такого процесса, в результате которого тело охладилось бы до температуры T = 0°К (принцип недостижимости абсолютного нуля температуры). 4. Принцип Нернста был развит Планком, предположившим, что S0 = 0: при абсолютном нуле температуры энтропия системы равна нулю. Физическое истолкование принципа Нернста в формулировке Планка дается в статистической физике. Условие S0 = 0 при T = 0°К является следствием квантового характера процессов, происходящих в любой системе при низких температурах, и выполняется только для систем находящихся при Т = 0°К в состоянии устойчивого, а не метастабильного равновесия. На основании гипотезы Планка можно определить абсолютные значения энтропии системы в произвольном равновесном состоянии.
19. Магнитное поле






25. Идеальный и реальный колебательные контуры
.Свободные колебания в идеальном контуре
Рассмотрим
вначале колебательный контур, в котором
отсутствуют потери электрической
энергии, то есть контур из идеальной
катушки индуктивности и идеального
конденсатора. Зарядим однократно
конденсатор от внешней батареи до
напряжения ![]() .
При этом электрическая энергия, запасенная
конденсатором, будет равна
.
При этом электрическая энергия, запасенная
конденсатором, будет равна
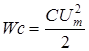 (3.45)
(3.45)
За счет разряда конденсатора через катушку индуктивности происходит преобразование электрической энергии в магнитную энергию. При этом магнитная энергия, запасенная катушкой индуктивности, становится равной
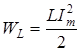 . (3.46)
. (3.46)
Затем
происходит обратное преобразование
магнитной энергии в электрическую
энергию. В результате в контуре происходит
колебательный процесс на некоторой
частоте ![]() , Которая
называется резонансной частотой. Такие
колебания называются свободными. Найдем
частоту свободных колебаний из равенства
электрической и магнитной энергий:
, Которая
называется резонансной частотой. Такие
колебания называются свободными. Найдем
частоту свободных колебаний из равенства
электрической и магнитной энергий:
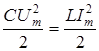 . (3.47)
. (3.47)
Учитывая,
что ![]() ,
подставим значение
В
предыдущее выражение:
,
подставим значение
В
предыдущее выражение:
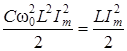 (3.48)
(3.48)
Отсюда резонансная частота колебаний
![]() , (3.49)
, (3.49)
А период колебаний
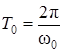 . (3.50)
. (3.50)
Из
равенства энергий найдем волновое
(характеристическое) сопротивление
контура ![]() :
:
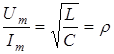 .
(3.51)
.
(3.51)
На резонансной частоте модуль реактивного сопротивления катушки индуктивности равен модулю реактивного сопротивления конденсатора:
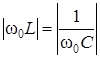 (3.52)
(3.52)
Подставляя значение резонансной частоты в выражения для модулей реактивных сопротивлений, получим:
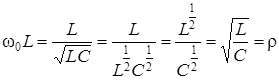 , (3.53)
, (3.53)
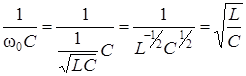 =
=![]() (3.54)
(3.54)
Таким образом, на резонансной частоте сопротивления реактивных элементов контура равны волновому сопротивлению. В идеальном контуре колебания будут незатухающими.
