4. Прикладные задачи имитационного моделирования

4.1. Ориентированный процесс случайного блуждания как метод прогнозирования

Применение аналитических и статистических моделей связано с априорным поиском структуры этих моделей чаще всего при ограниченной информации о характере развития процесса. Опре­деление параметров статистической модели и оценка точности прогноза требуют к тому же наличия необходимых статистических данных, характеризующих поведение объекта на периоде основания прогноза. Указанные обстоятельства в первую очередь снижают достоверность выводов в задачах прогнозирования разви­тия технических систем.

Для выполнения прогноза предлагается подход, не связанный с использованием жесткой структуры модели и серьезными требо­ваниями к объему априорной информации. Сущность метода за­ключается в представлении используемого для прогнозирования динамического ряда в качестве определенным образом ориентиро­ванного процесса случайного блуждания.

Значение изменяющегося параметра объекта прогнозирования для каждого момента на периоде основания можно представить в виде

,

где – значение динамического ряда в -й момент времени (год) периода основания;

– значение динамического ряда в предыдущий момент времени;

– приращение переменной объекта прогнозирования в -й момент времени по сравнению с предыдущими;

– число значений динамического ряда.

Поскольку приращения носят случайный характер, для них можно определить вид закона распределения и его параметры. При этом нужно учесть характер зависимости последующих при­ращений от предыдущих.

Предполагается, что в период упреждения характер изменения динамического ряда сохраняется. Тогда, используя характеристи­ки приращений, метод статистических испытаний можно применить для моделирования приращений в период упреждения прогноза. Значение единичной реализации прогноза на каждом последую­щем шаге прогнозирования будет

,

где – номер шага на периоде упреждения;

– число шагов на периоде упреждения;

– значение переменной объекта прогнозирования на пре­дыдущем шаге;

– моделируемое значение приращения на -м шаге.

Производя данную процедуру до момента прогнозирования, по­лучим значение точечного прогноза

,

где – точечный прогноз на -й период упреждения;

– конечное значение динамического ряда.

При разыгрывании данной процедуры многократно образуется совокупность случайных значений точечного прогноза. По полу­ченной выборке значений определяются среднее значение про­гноза и его дисперсия:

; (4.1)

, (4.2)

где – число реализаций точечного прогноза;

– разыгрываемое значение приращения на -м шаге периода упреждения в -й реализации точечного про­гноза;

– значение -й реализации точечного прогноза, опреде­ляемое по зависимости (1).

Рис. 4.1. Графическое отображение процесса случайного блуждания

Таким образом, процедура прогнозирования сводится к много­кратной имитации приращений на периоде упреждения и после­дующему определению статистических характеристик (среднего и дисперсии) реализаций точечного прогноза. График предлагаемо­го метода показан на рис. 4.1.

Как видно из изложенного, процедура определения характе­ристик прогноза при предлагаемом подходе отличается простотой, но вместе с тем характеризуется некоторой громоздкостью, обус­ловленной применением метода статистических испытаний. Поэтому коренным вопросом является рациональное моделирование приращений.

При наличии динамических рядов, имеющих продолжительный период основания, позволяющий получить репрезентативную вы­борку приращений, моделирование можно осуществлять в соот­ветствии с определенным по этой выборке эмпирическим законом распределения приращений.

Для коротких динамических рядов можно применить допуще­ние о нормальности отклонений значений динамического ряда от тренда. При этом допущении плотность распределения прираще­ний также является нормальной.

При наличии на периоде основания информации малого объ­ема (короткие динамические ряды) для моделирования прираще­ний целесообразно использовать двумерное нормальное распре­деление. Двумерная плотность вероятности зависит в этом случае от пяти параметров:

,

где – случайные значения, математические ожидания и среднеквадратические от­клонения предыдущих и последующих приращений переменной объекта про­гнозирования соответственно; – коэффициент корреляции последующих приращений на предыдущие.

Рис. 4.2. График определения предыдущих и последующих приращений

Графически определение предыдущих и последующих прира­щений показано на рис. 4.2.

Очевидно, что одно и то же приращение в зависимости от того, относительно какой точки оно рассматривается, может быть как предыдущим, так и последующим. Однако первое приращение яв­ляется только предыдущим.

При обработке исходного динамического ряда определяются оценки математических ожиданий и дисперсий предыдущих и последующих приращений. Множество предыдущих приращений определяется по зависимости

.

Множество последующих приращений определяется по зависимости

или

.

По множеству определяются среднее значение и оценка дисперсии предыдущих приращений:

(4.3)

Соответственно, по множеству определяются среднее значе­ние и оценки дисперсии последующих приращений:

(4.4)

Оценка значения коэффициента корреляции определится по зависимости

. (4.5)

Для моделирования случайных приращений на периоде упреж­дения используется алгоритм моделирования двумерного нормаль­ного распределения. Для рассматриваемого случая моделирующая зависимость последующих приращений имеет вид

(4.6)

При моделировании случайного значения на первом шаге в каждой -й реализации предыдущее значение равно значению последнего приращения на периоде основания ,то есть

При моделировании приращений на следующих шагах перио­да упреждения

.

Оценка коэффициента корреляции, определяемая по выборкам малых объемов, является случайной. Плотность вероятности выбо­рочного коэффициента корреляции имеет сложный вид. При приня­том допущении о нормальности распределения приращений исполь­зуется нормализующее преобразование Фишера.

Случайная величина распределена нормально с параметрами

; (7)

,

где – значение выборочного коэффициента корреляции, опреде­ляемое по зависимости (4.5).

Моделируем значения как нормально распределенную слу­чайную величину по зависимости

, (4.8)

где – нормированная нормально распределенная случайная ве­личина, моделируемая с помощью алгоритма.

Осуществляя обратный по отношению к преобразованию Фише­ра переход, получим случайное значение коэффициента корреля­ции

. (4.9)

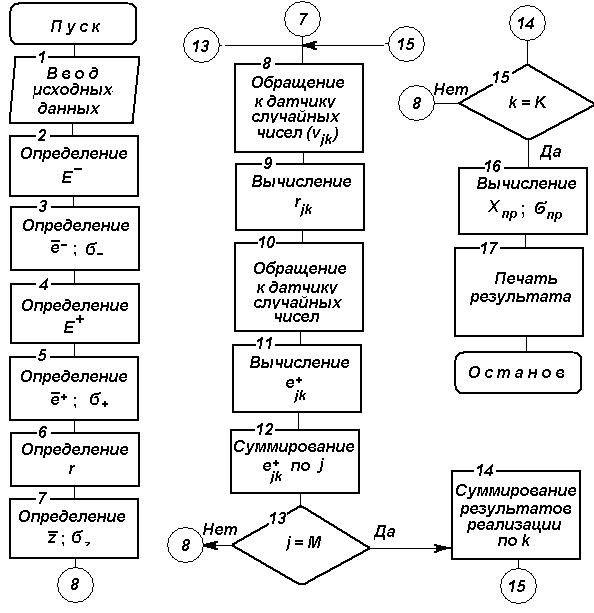
Рис. 4.3. Блок-схема алгоритма прогнозирования с использованием ориентированного процесса случайного блуждания

С учетом изложенного моделирование приращений на периоде упреждения включает выполнение следующих действий:

1. обращение к датчику нормированных нормально распределенных случайных чисел и получение ;

2. вычисление случайного значения по зависимостям (4.8) и (4.9);

3. обращение к датчику равномерно распределенных случайных чисел и получение числа ;

4. вычисление приращения по зависимости (4.6) при полученном в п. 2 значении коэффициента корреляции , определенном в п. 3 значении .

Многократно имитируя приращения и используя зависимости (4.1) и (4.2), вычисляются характеристики прогноза. Блок-схема алгоритма изображена на рис.4.3.

К достоинствам рассмотренного метода прогнозирования отно­сятся:

• простота вычислительного алгоритма;

• возможность использования при ограниченной на периоде осно­вания информации (начиная с 7-9 значений динамического ряда);

• простота оценивания точности прогноза (определения диспер­сии).