13. Графики iL и uc расситанных методом переменных состояния с помощью программы MathCad
Вот система уравнений и независимые начальные условия с которыми мы сейчас будем работать
Независимые начальные условия
Систему уравнений и независимые начальные условия запишем в матричном виде :
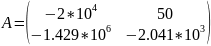
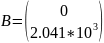
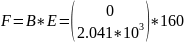
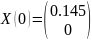
Где А - собственная матрица системы; В – вектор коэффициентов при воздействиях; Х(0) – вектор независимых начальных условий; Е – величина входных воздействий.
В системе MathCAD программа интегрирования уравнений по методу Рунге – Кутта имеет имя Rkfixed. Обращение к ней производится через оператор присвоения какой-либо переменной (например, Z) имени программы:
Где Х – вектор
переменных состояния, размер которого
определяется вектором независимых
начальных значений Х(0) и соответствует
числу уравнений состояния; 0 и
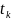- начало и конец временного интервала
интегрирования; n
– число точек на интервале интегрирования;
D
– функция, которая описывает правую
часть уравнений, разрешенных относительно
первых производных.
Для линейных цепей функция D – имеет вид линейного матричного преобразования:
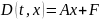
Все элементы матриц А и F должны быть определены перед обращением к программе Rkfixed.
Решение получается
в виде матрицы Z,
где первый столбец соответствует
дискретным значениям времени t.
остальные столбцы соответствуют
значениям переменных состояния.
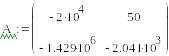
А теперь сделаем проверку собственных чисел
Вывод:
Собственные числа матрицы равны корням характеристического уравнения, значит расчеты верны.
Важно так же отметить что при апериодическом процессе (корни характеристического уравнения вещественные) графики строят для промежутка времени:
,
где
-
наибольшая постоянная времени, полученная
при расчете свободной составляющей:
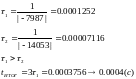
14. Графики токов и напряжений рассчитанных классическим методом
Графики токов
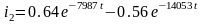
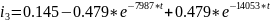
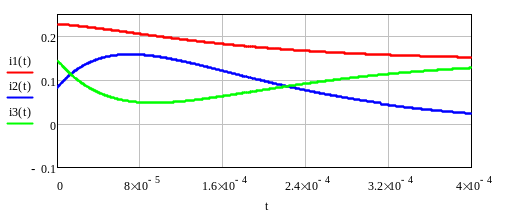
Проверка
Для момента
t=0.0001c
Все сошлось .Расчет верен
Графики напряжений
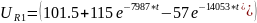
Проверка
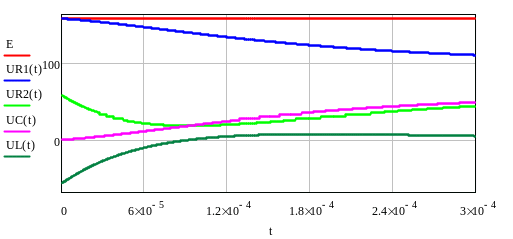
Для момента t=0.0001c
Все сошлось. Расчет верен
15.Список литературы
«Электротехника: домашние и курсовые задания». Изд. 2-е, испр./Под ред. П.А.Галайдина; БГТУ – СПб., 2007 г.
Нейман Л.Р., Демирчян К.С. «Теоретические основы электротехники». Ленинград. Энергоиздат. Ленинградское отделение, 1981 г.
Бессонов Л.А. «Теоретические основы электротехники. Электрические цепи». 9-е изд., перераб. и доп. – М.: «Высшая школа», 1996г
Теория из тетради с лекций.
Мое мнение о проделанной работе:
Хочу начать с того, что сотворить такое чудо, да еще и самому, это очень приятно, даже если учесть что пришлось потратить не малое количество времени на его создание и проверку достоверности всех результатов.
Курсовая работа – это дело ответственное, и к нему нужно найти особый подход. Лично я долго оттягивал это до тех пор, пока мы на практическом занятии не разобрали расчет методом Д-Алгебраизации и Операторным методом, так как я очень люблю математику, мне стало интересно, ее применение в Электротехнике. Я стал разбираться в сути методов, и загорелся сделать всю работу как можно скорее. Очень еще понравилось работать с графиками, с использованием метода Рунге-Кутта.
В общем работа хоть и была объемной, важно сказать, что я в целом от себя, и от своей работы доволен. Надеюсь что многие согласятся со мной.
Хочется пожелать студентам, которые будут работать над такой же Курсовой удачи!