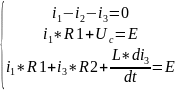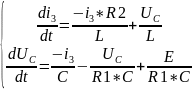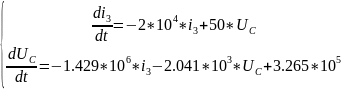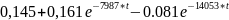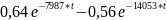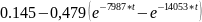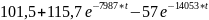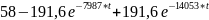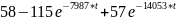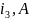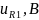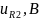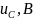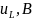- •Переходные процессы в электрических цепях. Вариант №11-160-
- •1.Схема и параметры цепи
- •2. Составление характеристического уравнения по Zвх
- •3. Определение принуждённых составляющих
- •4. Определение начальных условий
- •5. Составление дифференциального уравнения
- •6. Составление дифференциального уравнения
- •7. Анализ полученного дифференциального уравнения
- •При расчете принужденных составляющих мы получили:
- •8. Решение ду классическим методом относительно iL
- •9.Определение остальных токов и напряжений
- •10.Проверочная Таблица
- •11. Операторный метод расчета
- •12. Расчет переходного процесса методом переменных состояния
- •13. Графики iL и uc расситанных методом переменных состояния с помощью программы MathCad
- •14. Графики токов и напряжений рассчитанных классическим методом
- •15.Список литературы
8. Решение ду классическим методом относительно iL


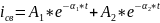
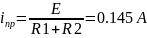
Независимое начальное условие
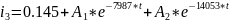
Пусть t=0 тогда:
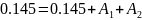
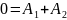



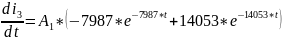
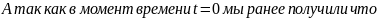


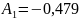
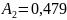

9.Определение остальных токов и напряжений


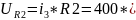
10.Проверочная Таблица
t→∞ |
По уравнениям |
0,145 |
0 |
0,145 |
101,5 |
58 |
58 |
0 |
|||||||
По законам Кирхгофа |
E/(R1+R2)=0,145
|
0
|
E/(R1+R2)=0,145
|
E*R1(R1+R2)=101,5 |
i3*R2 = 58
|
i3*R2 = 58
|
0 |
||||||||
t=0 |
По уравнениям |
0,228 |
0,083 |
0,145 |
160 |
58 |
0 |
-58 |
|||||||
По законам Кирхгофа |
E/R1= 0,228 |
i1-i3 = 0,083 |
|
i1*R1 = 160 |
i3*R2 = 58 |
|
-i3*R2 =-58 |
||||||||
t<0 |
E/(R1+R2)=0,145 |
0 |
E/(R1+R2)=0,145 |
E*R1/(R1+R2)=101,5 |
E*R2/(R1+R2)=58 |
|
0 |
||||||||
Уравнение |
|
|
|
|
|
|
|
||||||||
Величина |
|
|
|
|
|
|
|
||||||||
11. Операторный метод расчета

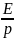 R1
R1
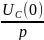 I1(p)
I1(p)
 I2(p)
I2(p)
L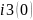 I3(p)
I3(p)
pL R2

Найдем
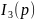 используя метод Крамера
используя метод Крамера
Главный определитель

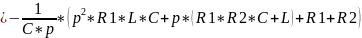

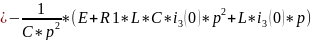
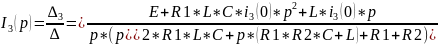 (11.3)
(11.3)
По
теореме разложения находим оригинал –
закон изменения искомой переменной. В
простейших случаях оригинал можно
находить по формулам соответствия:
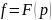
Воспользуемся формулой разложения

Где
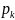 – корни уравнения
– корни уравнения

Для полученного выражения (11.3)
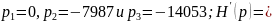

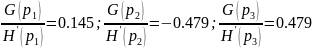
Подстановка в формулу разложения дает:

12. Расчет переходного процесса методом переменных состояния
В основе метода переменных состояния лежит запись исходной системы дифференциальных уравнений (4.3.1-4.3.3.) в канонической форме Коши.При этом в качестве переменных состояния принимаем токи в катушках индуктивности и напряжения на конденсаторах, которые однозначно определяют запас энергии в любой момент времени. Переходный процесс в рассматриваемой цепи описывается системой дифференциальных уравнений в форме Коши и системой независимых начальных условий.
Е R1
i1
C i2
i3
L R2