Билет 1
1 ) Распределение Максвелла - распределение по скоростям (или импульсам) молекул системы, находящейся в состоянии термодинамического равновесия.
называется функцией распределения молекул по скоростям или законом Максвелла.
Экспериментальная проверка закона распределения Максвелла - опыт Штерна
В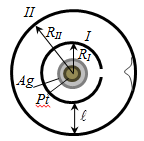
доль
оси внутреннего цилиндра с целью натянута
платиновая проволока, покрытая слоем
серебра, которая нагревается током.
При нагревании серебро испаряется,
атомы серебра вылетают через щель и
попадают на внутреннюю поверхность
второго цилиндра. Если оба цилиндра
неподвижны, то все атомы независимо от
их скорости попадают в одно и то же место
В. При вращении цилиндров с угловой
скоростью ω атома серебра попадут в
точки В’, B’’ и так далее. По
величине ω, расстоянию ? и смещению х =
ВВ’ можно вычислить скорость атомов,
попавших в точку В’.
Изображение щели получается размытым. Исследуя толщину осаждённого слоя, можно оценить распределение молекул по скоростям, которое соответствует максвелловскому распределению.
2)
ВОЛНОВОЕ
ЧИСЛО -
модуль волнового
вектора; определяет
пространственный период волны (длину
волны 
)
в направлении её распространения: 
(где 
-
круговая частота, 
-
фазовая скорость волны). В оптике и
спектроскопии волновое число часто
наз. величину, обратную длине волны,
.
ВОЛНОВОЙ
ВЕКТОР -
вектор k,
определяющий направление распространения
и пространственный период плоской
монохроматич. волны:
где 
-
постоянные амплитуда и фаза волны, 
-
круговая частота, r -
радиус-вектор. Модуль В. в. наз. волновым
числом k=
,
где 
-
пространственный период или длина
волны. В направлении В. в. происходит
наибыстрейшее изменение фазы волны 
,
поэтому оно и принимается за направление
распространения.
3) Тепловая машина за один цикл совершает работу равную 3 кДж и отдает холодильнику кол-во теплоты 12 кДж. Определить КПД.
Билет 2
1) Второй закон — второе начало термодинамики: Второй закон термодинамики исключает возможность создания вечного двигателя второго рода. Имеется несколько различных, но в то же время эквивалентных формулировок этого закона.
1 — Постулат Клаузиуса. Процесс, при котором не происходит других изменений, кроме передачи теплоты от горячего тела к холодному, является необратимым, то есть теплота не может перейти от холодного тела к горячему без каких-либо других изменений в системе. Это явление называют рассеиванием или диссипацией энергии.
Приведем второе начало
термодинамики в ещё одной формулировке Рудольфа
Юлиуса Клаузиуса (1865):
для любой квазиравновесной термодинамической
системы существует однозначная функция
термодинамического состояния 
,
называемая энтропией, такая, что ее
полный дифференциал 
. [3]
2 — Постулат
Кельвина. Процесс,
при котором работа переходит в теплоту
без каких-либо других изменений в
системе, является необратимым, то есть
невозможно превратить в работу всю
теплоту, взятую от источника с однородной
температурой, не проводя других изменений
в системе.
Например,
возьмем два тела с различной температурой
(нагреватель и холодильник) и проведем
несколько циклов тепловой
машины,
забрав тепло 
у
нагревателя, отдав 
холодильнику
и совершив при этом работу 
.
После этого воспользуемся процессом
Клаузиуса и вернем тепло
от
холодильника нагревателю. В результате
получается, что мы совершили работу
только за счет отъёма теплоты от
нагревателя, то есть постулат Томсона
тоже неверен.
В
статистической
термодинамике, уравнение
Больцмана связывает
энтропию 
идеального
газа и термодинамическую
вероятность — величину 
,
которая равна количеству микросостояний,
соответствующих данному макро
состоянию системы:
,
где 
— постоянная
Больцмана, равная 
[Дж/К].
Иначе говоря, формула Больцмана показывает отношение между энтропией и числом способов конструирования данной системы из атомов или молекул.
2) Уравнение состояния вещества— уравнение, связывающее между собой термодинамические (макроскопические) параметры системы, такие, как температура, давление, объём, химический потенциал и др. Уравнение состояния можно написать всегда, когда можно применять термодинамическое описание явлений.
3) Определить отношение ср.кв. скоростей молекул гелия и азота при одинаковых температурах.