4 Часть 3.
4. 1 Коррекция сау.
С
целью обеспечения устойчивости вводят
форсирующее звено с передаточной
функцией. Обычно форсирующее звено
образуют с помощью
параллельного соединения имеющегося системе интегратора и безынерционного звена.
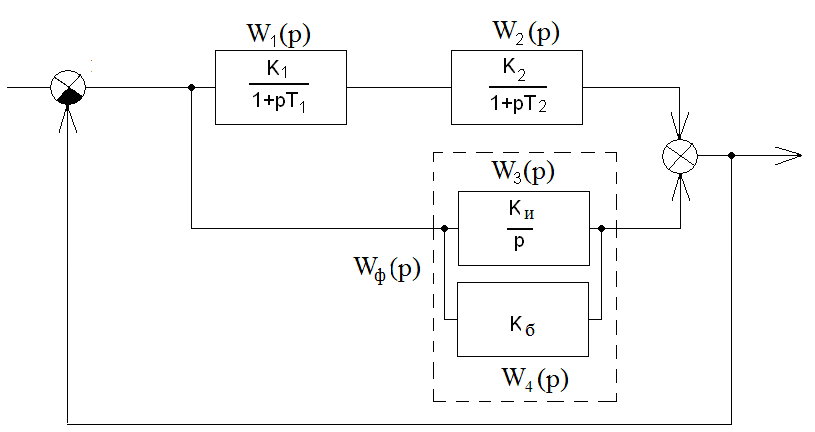
Рисунок 30. Структурная скорректированная схема.
;
;
;
;
Таким образом, при
заданной постоянной времени форсирующего
звена и известном коэффициенте усиления
можно
определить коэффициент передачи
безынерционного звена
.
Постоянная
времени
форсирующего звена
определяется с помощью анализа
логарифмической АЧХ (ЛАЧХ) разомкнутой
САУ. При этом выбор
обычно производится
таким образом, чтобы на частоте среза
(
)
наклон ЛАЧХ составлял минус 20дБ/дек
на участке
в 1-2 декады от частоты среза.
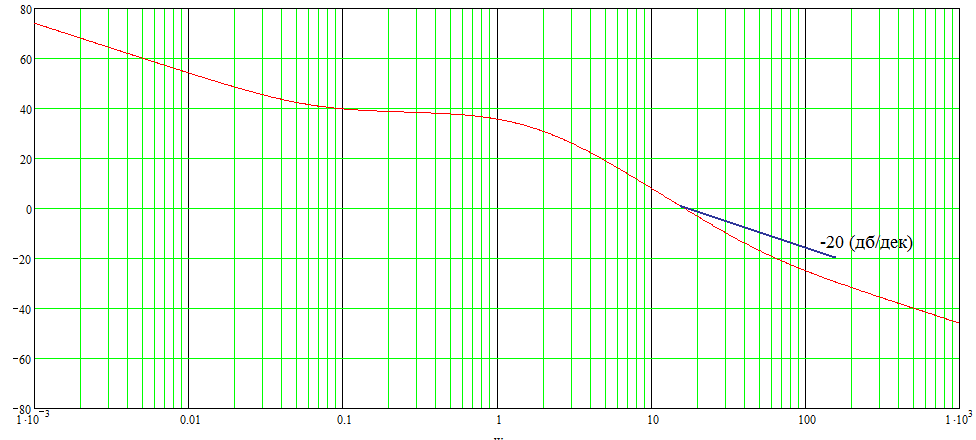
Рисунок 31. ЛАЧХ разомкнутой системы.
Из графика видно,
что
,
то
,
следовательно
.
;
;
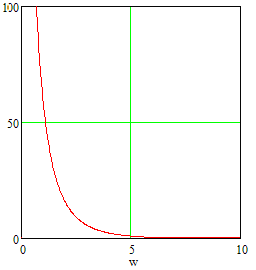
Рисунок 32. Передаточная характеристика скорректированной системы.
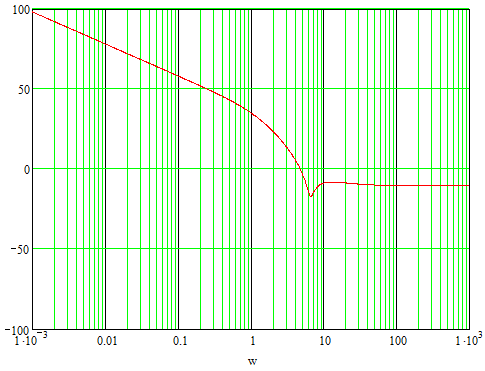
Рисунок 33. ЛАЧХ скорректированной системы.
4. 2 Определение скорректированной системы на устойчивость.
Определение устойчивости по расположению корней на комплексной плоскости
Для анализа системы на устойчивость найдем корни характеристического уравнения:
;
Корни:
Т.к. корни имеют реальные значения и к тому же отрицательные, то, исходя из основного условия устойчивости, можно утверждать, что система устойчива.
Критерий
Найквеста.
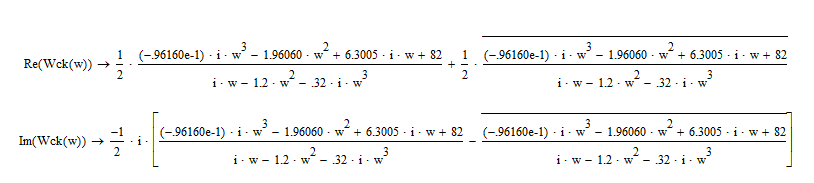
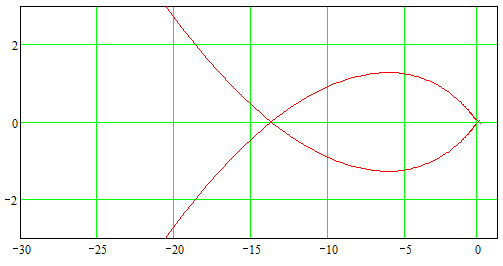
Рисунок 34. Годограф скорректированной системы.
Критерий Гурвица.
Запишем характеристическое уравнение:
;
Матрица Гурвица имеет вид ;
Вычислим определители , , .
Система устойчива, т. к. все определители матрицы Гурвица положительны.
Определение запаса устойчивости усилению и по фазе.
Разомкнутой системы.
Т. к.
,
при
то запас по усилению (амплитуде)
.
Т. к.
,
то запас устойчивости по фазе
.
Вывод.
Таким образом в моделировании систем автоматического регулирования отправной точкой является передаточная функция разомкнутой системы. Первым из способов моделирования является, так сказать, разложение этой передаточной функции на составляющие, а затем определение схемотехнического вида каждой из совокупности передаточных функций. Вторым же способом является определение операций над сигналами, т.е. после всех преобразований дифф. уравнения, составленного из передаточной функции разомкнутой системы, находятся, так сказать, промежуточные сигналы, которые и определяют сначала структурный, а затем и схемотехнический облик системы на АВМ.
Данная работа представляет собой реализацию двух этих методов. Несмотря на наличие и новых, более точных методов, как численные методы, эти два способа анализа и синтеза систем на АВМ, наиболее пригодны для ручного использования (т.е. без ЭВМ). Однако они не дают 100% - ной точности в расчетах. Однако на практике, в большинстве случаев, этого оказывается достаточно.
Таким образом были рассмотрены фундаментальные методы анализа и синтеза систем на АВМ и создание цепей коррекции.
