2. 9 Расчет цепи коррекции.

Необходимо создать такую цепь коррекции, чтобы , и запас по усилению (амплитуде) .

Коэффициент передачи разомкнутой системы:

;

Преобразуем:

Чтобы построить график передаточной функции запишем коэффициент передачи в комплексной форме:

;

Строим графики ЛАЧХ и ЛФЧХ:

Рисунок 22. Графики ЛАЧХ и ФЧХ.

Где:

, , , , т. е. ;

, - нескорректированные соответственно ЛАЧХ и ЛФЧХ.

, - скорректированные соответственно ЛАЧХ и ЛФЧХ.

Т. к. , то получим следующие графики:

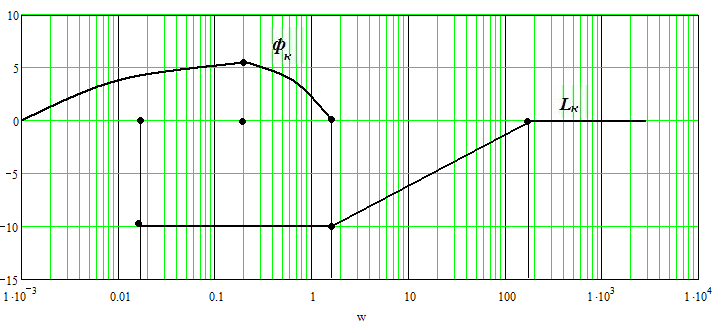
Рисунок 22. Корректирующие ЛАЧХ и ЛФЧХ.

Полученная корректирующего устройства соответствует последовательному соединению упруго дифференцирующего контура и дополнительного усилителя. Передаточная функция которого:

;

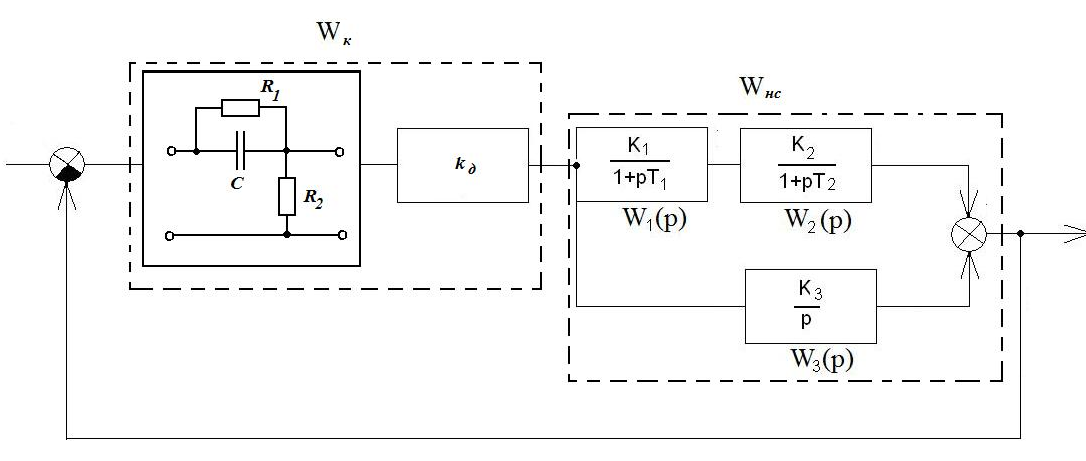
Рисунок 23. Схема с коррекцией.

Рассчитаем параметры корректирующей схемы:

; ; .

3 Часть 2.

3. 1 Построение схемы устройства на авм по структурной схеме.

Т.к. имеется передаточная функция для каждого звена в разомкнутом состоянии, то запишем все три передаточных функции и проанализируем их:

; ; ;

Очевидно, что выполняет интегрирование сигнала, а и выполняют однотипные действия. Так же очевидно, что в цепи О.С. схем с передаточными функциями вида , и должен быть нелинейные, а так же линейные элементы. Поэтому для передаточных функций и справедлива следующая схема:

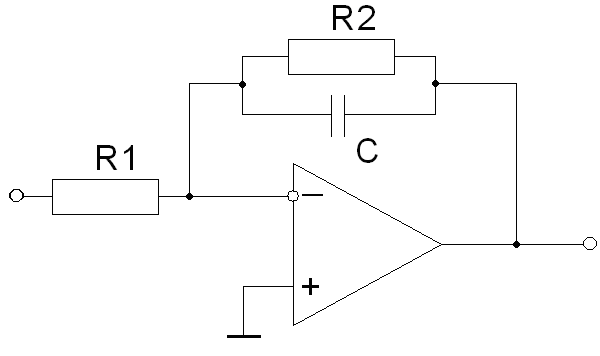
Рисунок 26. Общая схема передаточных функций и .

Чтобы доказать справедливость выбранного звена для передаточных функций и , найдем передаточную функцию звена, показанного на Рисунке 26:

;

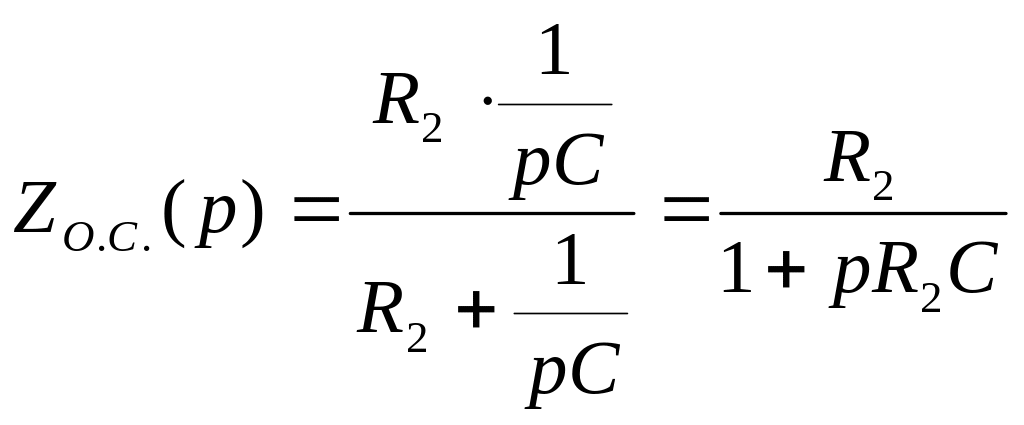Т.к. схема на Рисунке 26 построена по принципу инвертирующего усилителя, то коэффициент передачи можно записать:

;

Что и требовалось доказать.

Интегрирующее звено будет иметь следующий вид:

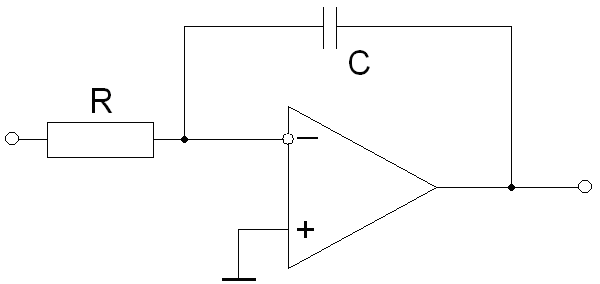
Рисунок 27. Схема интегрирующего звена.

Как видно из Рисунок 27. интегрирующее звено тоже построено по схеме инвертирующего усилителя.

Т.к. в наличии уже имеются все звенья передаточных функций, то согласно Рисунку 1. построим схему на АВМ по передаточной функции каждого звена:

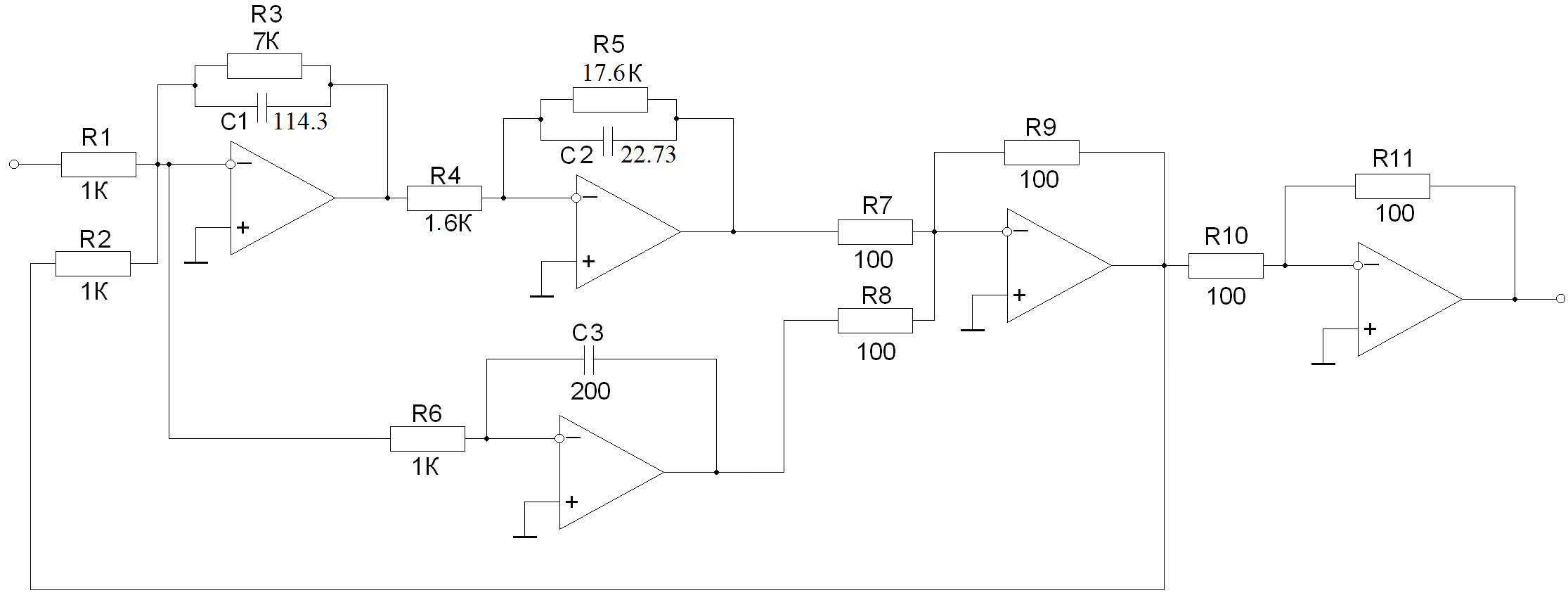
Рисунок 28. Принципиальная схема на АВМ, построенная по передаточной функции.

Первые три ОУ выполняют соответственно функции, которые описаны в , и . Четвертый ОУ используется для сложения сигналов от трех ОУ, и имеет коэффициент передачи равный единице. Пятый ОУ инвертирует выходной сигнал, чтобы его полярность оставалась такой же как и на входе, и соответственно тоже имеет единичный коэффициент передачи.

Номиналы элементов определяются из следующих соотношений:

;

Пусть , то , ;

Пусть , то , а ;

, то ;

Пусть , то ;

Пусть , то ;

3. 2 Построение схемы устройства на авм по дифференциальному уравнению передаточной функции системы.

Построение принципиальной схемы целесообразно проводить по передаточной функции всей системы в разомкнутом состоянии. Для начала запишем передаточную функцию системы в разомкнутом виде:

; (1)

Известно, что умножение на оператор Лапласа р производит дифференцирование выражения столько раз, сколько раз этот оператор умножается на выражение. Поэтому переход от функции оператора Лапласа к дифференциальному уравнению легко производится вручную.

Зная, что , запишем дифференциальное уравнение разомкнутой системы:

;

Преобразуем данное выражение:

; (2)

; (3)

Данному выражению соответствует дифференциальное уравнение:

; (4)

Где предварительно была введена замена .

Выражение (2) имеет общий вид:

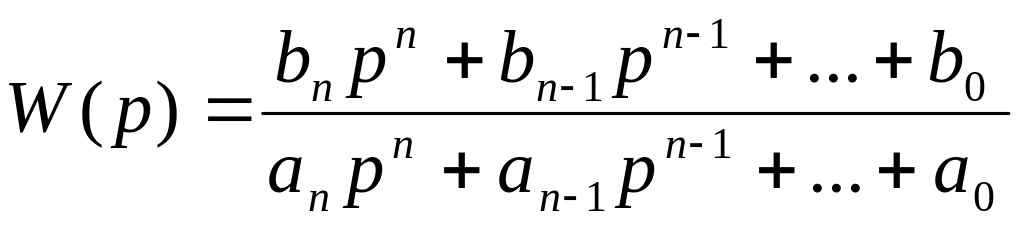; (5)

Поэтому, исходя из выражения для дифференциального уравнения системы (3), можно для системы 3-его порядка записать следующие коэффициенты:

(6)

Введем обозначение (6.1), и оставим систему дифференциальных уравнений:

(7)

Подставим коэффициенты в систему (7) и получим:

(8)

Выразив из первого уравнения системы (8) и подставив его во все остальные уравнения, получим:

(9)

Продеффиренцируем систему (9) , чтобы записать следующее дифференциальное уравнение:

(10)

Подставим в данное уравнение замену (10) и, раскрыв знаки суммы, получим следующее уравнение:

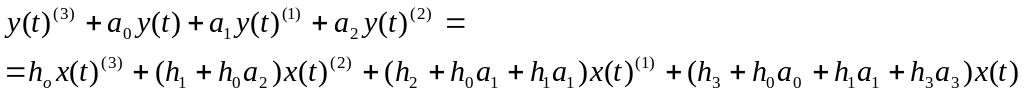(11)

Учитывая систему коэффициентов (6), найдем коэффициенты :

(12)

Теперь, зная значения коэффициентов , и , запишем систему уравнений (7), но уже с известными коэффициентами:

(13)

А также запишем выражение для замены, с учетом того, что :

; (14)

Теперь вернемся к изначальному обозначению входных и выходных сигналов, учитывая, что

; (15)

Учитывая соотношения (14) и (15) можно записать систему дифференциальных уравнений связи входных и выходных сигналов:

(16)

В системе (16) играют роль внутрисистемных промежуточных сигналов, так же в дополнение к системе (16) можно записать еще одну, которая будет указывать на операции, что необходимо провести над сигналами, чтобы получить тот или иной сигнал. Назовем её системой связи:

(17)

Итак, схема на АВМ, построенная по дифференциальному уравнению будет иметь вид:

Рисунок 29. Принципиальная схема на АВМ, построенная по дифф. уравнению.

На схеме введены следующие обозначения:

И – инвертор (коэффициент усиления единица);

- интегратор (коэффициент усиления единица);

Так же имеются ОУ, в которых обозначены коэффициенты h или a, это обычные усилители с усилением в а или h раз.

Номиналы элементов определяются из следующих соотношений:

(18)

Найдем номиналы элементов:

Пусть , то ;

Пусть , то ;

Пусть , то ;

Пусть , то ;

Пусть , то ;

Пусть , то ;

Пусть , то ;

Пусть , то ;

Все номиналы элементов, рассчитанных в этом пункте, приведены на Рисунке 29.