
- •Курсовая работа
- •Часть 2: Составить математическую модель системы на авм по структурной схеме и дифференциальному уравнению.
- •Часть 3: Коррекция сау. Определение скорректированной системы на устойчивость. Содержание.
- •Введение.
- •1 Исходные данные.
- •2 Часть 1.
- •2. 1 Передаточная функция разомкнутой системы.
- •2. 2 Передаточная функция замкнутой системы.
- •2. 3 Определение устойчивости.
- •2. 3. 1 По расположению корней на комплексной плоскости.
- •2. 3. 2 По критерию Гурвица.
- •2. 3. 3 Критерий Михайлова.
- •2. 5 Импульсная переходная функция замкнутой системы.
- •2. 6 Переходная характеристика замкнутой системы.
- •2. 7 Импульсная переходная характеристика разомкнутой системы.
- •2. 8 Определение частотных показателей качества переходного процесса.
- •2. 9 Расчет цепи коррекции.
- •3 Часть 2.
- •3. 1 Построение схемы устройства на авм по структурной схеме.
- •3. 2 Построение схемы устройства на авм по дифференциальному уравнению передаточной функции системы.
- •4 Часть 3.
- •4. 1 Коррекция сау.
- •4. 2 Определение скорректированной системы на устойчивость.
- •Определение запаса устойчивости усилению и по фазе.
- •Литература.
2. 5 Импульсная переходная функция замкнутой системы.
Импульсная переходная характеристика, или как её ещё принято называть, функция веса, ищется при действии на входе дельта функции Дирака, которая описывается следующим образом:

![]()
Так же у данной
функции есть еще одна особенность. Она
заключается в том, что при прямом
преобразовании Лапласа, т.е. переходе
в р
область, данная функция равна единице
на всем интервале существования интеграла
Лапласа, т.е. при p
больших или равных нулю. Поэтому можно
записать, что
![]() .
Запишем передаточную функцию замкнутой
системы:
.
Запишем передаточную функцию замкнутой
системы:
![]() ;
;
Т.к. , то
![]() ;
;
Применив обратное преобразование к выражению h(p), получим h(t):


 График
импульсной переходной функции разомкнутой
системы будет иметь вид:
График
импульсной переходной функции разомкнутой
системы будет иметь вид:
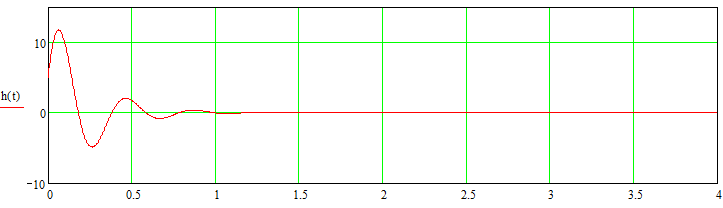
Рисунок 19. Импульсная переходная характеристика замкнутой системы q(t).
2. 6 Переходная характеристика замкнутой системы.
Нахождение q(t)
производится по передаточной функции
замкнутой системы H(p),
при действие на входе
![]() в p
– области
в p
– области
![]()
Запишем еще раз передаточную функцию H(p):
;
Тогда
;
Будем рассматривать
данное выражение на промежутке
![]() ,
что вполне удовлетворяет обратному
преобразованию Лапласа. Т.к.
,
что вполне удовлетворяет обратному
преобразованию Лапласа. Т.к.
![]() ,
а
,
а
![]() ,
то можно записать выражение для
,
то можно записать выражение для
![]() :
:
![]() ;
;
Из выражения видно,
что
![]() .
Через обратное преобразование Лапласа
найдем импульсную переходную характеристику
замкнутой системы:
.
Через обратное преобразование Лапласа
найдем импульсную переходную характеристику
замкнутой системы:


График будет иметь следующий вид:
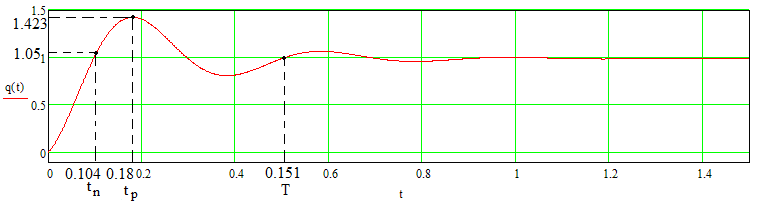
Рисунок 20. Переходная характеристика замкнутой системы q(t).
2. 7 Импульсная переходная характеристика разомкнутой системы.
Импульсная переходная характеристика, или как её ещё принято называть, функция веса, ищется при действии на входе дельта функции Дирака, которая описывается следующим образом:
![]()
Так же у данной функции есть еще одна особенность. Она заключается в том, что при прямом преобразовании Лапласа, т.е. переходе в р область, данная функция равна единице на всем интервале существования интеграла Лапласа, т.е. при p больших или равных нулю. Поэтому можно записать, что . Запишем передаточную функцию разомкнутой системы:
![]() ;
;
Т.к. , то
![]() ;
;
Применив обратное преобразование к выражению w(p), получим w(t):
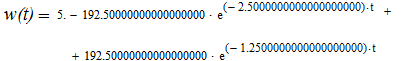
График функции w(t) будет выглядеть так:
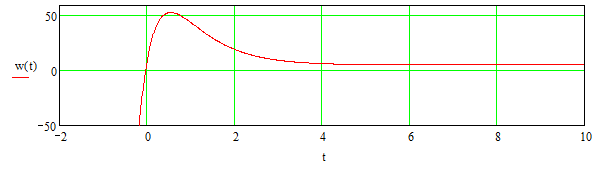
Рисунок 21. Импульсная переходная характеристика замкнутой системы w(t).
2. 8 Определение частотных показателей качества переходного процесса.
По переходной характеристике q(t) определим следующие показатели качества:
а) Длительность переходного процесса:
 Длительностью
переходного процесса называется время,
при котором амплитудное значение
переходного процесса не превышает 5% от
его установившегося значения.
Длительностью
переходного процесса называется время,
при котором амплитудное значение
переходного процесса не превышает 5% от
его установившегося значения.
 Из
графика q(t)
видно, что установившееся значение
переходного процесса
Из
графика q(t)
видно, что установившееся значение
переходного процесса
![]() .
Найдем время, при котором q(t)
будет равно 1,05. Из графика видно, что
.
Найдем время, при котором q(t)
будет равно 1,05. Из графика видно, что
![]() .
.
б) Перерегулирование:
Под перерегулированием
![]() подразумевается отношение максимального
значения выходного сигнала q(t)
к его установившемуся значению. Т.к.
установившееся значение в переходном
процессе равно единице, то достаточно
найти лишь максимальное значение сигнала
в переходном процессе:
подразумевается отношение максимального
значения выходного сигнала q(t)
к его установившемуся значению. Т.к.
установившееся значение в переходном
процессе равно единице, то достаточно
найти лишь максимальное значение сигнала
в переходном процессе:
![]() ;
;
По графику q(t) было найдено максимальное значение сигнала в переходном процессе, теперь можно найти перерегулирование:
![]() ;
;
в) Время установления первого максимума:
Из графика q(t)
видно, что первый максимум устанавливается
за время
![]() .
.
г) Частоту колебаний в переходном процессе:
Из графика q(t) найдем, что период колебаний T=0.51, тогда частота колебаний в переходном процессе:
![]() ;
;
По частотной
характеристике
![]() определим следующие показатели качества:
определим следующие показатели качества:
д) Полосу пропускания:
Полосу пропускания
будем искать по уровню 0,7 от максимального
значения
.
Из графика можно найти, что максимальное
значение, которое принимает АЧХ
передаточной функции замкнутой системы
равно 2 . Умножив данное число на 0,7 найдем
значения АЧХ при уровне 0,7 от его
максимального значения, оно будет
составлять 1.4 . Теперь, решив уравнение
![]() ,
найдем значение верхней и нижней
граничной частоты:
,
найдем значение верхней и нижней
граничной частоты:

![]()
Тогда полоса
пропускания
![]()
е) Резонансную частоту:
Как известно при максимальном коэффициенте передачи в системе наступает резонанс. Поэтому, решая уравнение , находим резонансную частоту:
![]()
ж) показатель колебательности:
Показатель колебательности М есть максимальное значение АЧХ передаточной функции замкнутой системы. Из графика видно, что М=2;
