2. 2 Передаточная функция замкнутой системы.

Т.к. в моем случае имеется О.О.С. и коэффициент передачи цепи обратной связи равен единице, то можно записать передаточную функцию замкнутой системы как:

;

После подстановки W(p) в выше стоящее выражения и его упрощения получим:

;

Запишем данную передаточную функцию в комплексной форме:

;

Найдем модуль данной комплексной формы передаточной функции:

;

;

Графики будет иметь вид:

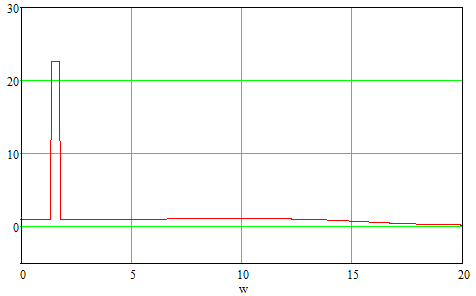
Рисунок 7. Передаточная характеристика замкнутой системы.

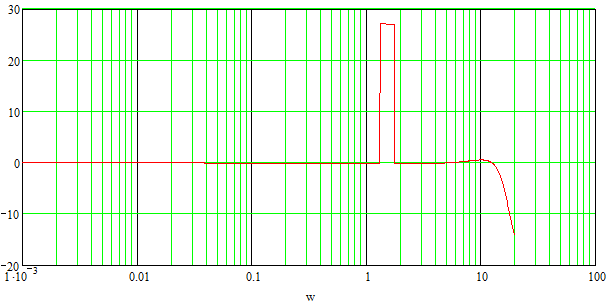
Рисунок 8. ЛЧХ замкнутой системы.

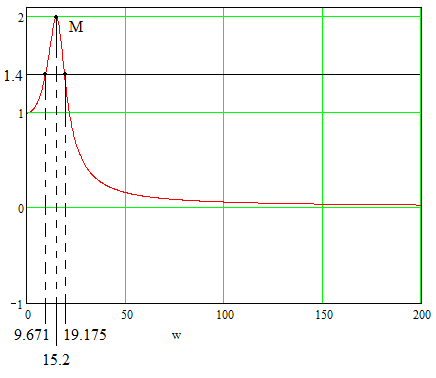
Рисунок 9. АЧХ замкнутой системы.

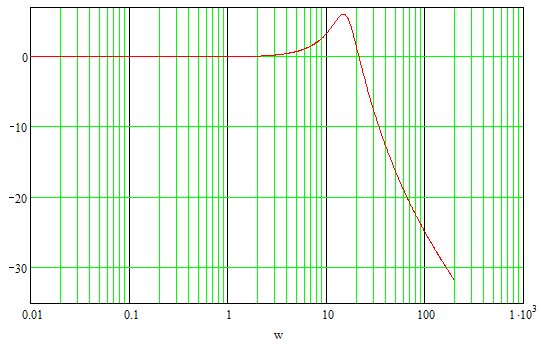
Рисунок 10. ЛАЧХ замкнутой системы.

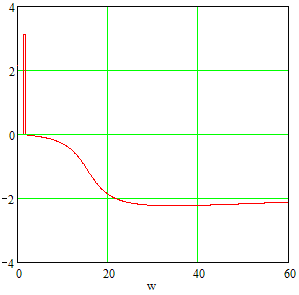
Рисунок 11. ФЧХ замкнутой системы.

Рисунок 12. ЛФЧХ замкнутой системы.

2. 3 Определение устойчивости.

2. 3. 1 По расположению корней на комплексной плоскости.

Определение устойчивости по расположению корней на комплексной плоскости разомкнутой системы.

Для анализа системы на устойчивость найдем корни характеристического уравнения:

;

Корни:

Т.к. корни имеют реальные значения и к тому же отрицательные, то, исходя из основного условия устойчивости, можно утверждать, что система устойчива.

Т. к. корни характеристического уравнения разомкнутой системы действительные, то система не является колебательной.

Устойчивость данной системы .

Определение устойчивости по расположению корней на комплексной плоскости замкнутой системы.

Найдем корни характеристического уравнения передаточной функции, чтобы проанализировать систему на устойчивость:

;

Корни:

Т.к. действительные части корней отрицательны, то, исходя из основного условия устойчивости, можно утверждать, что система устойчива.

Т. к. имеются мнимые части корней, то система колебательная.

Устойчивость данной системы .

2. 3. 2 По критерию Гурвица.

Определение устойчивости по критерию Гурвица разомкнутой системы.

Запишем характеристическое уравнение:

;

Матрица Гурвица имеет вид ;

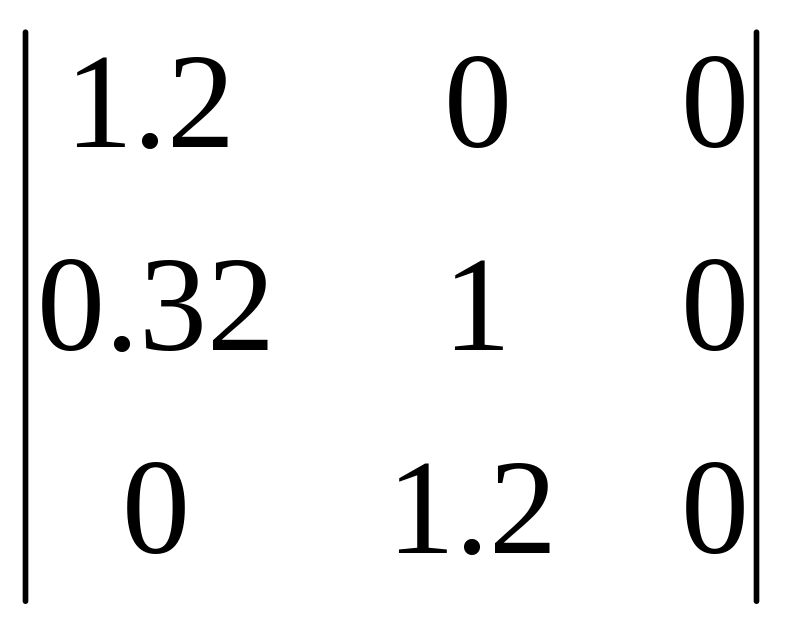Вычислим определители , , .

Система устойчива, т. к. все определители матрицы Гурвица положительны.

Определение устойчивости по критерию Гурвица замкнутой системы.

Запишем характеристическое уравнение:

;

Матрица Гурвица имеет вид ;

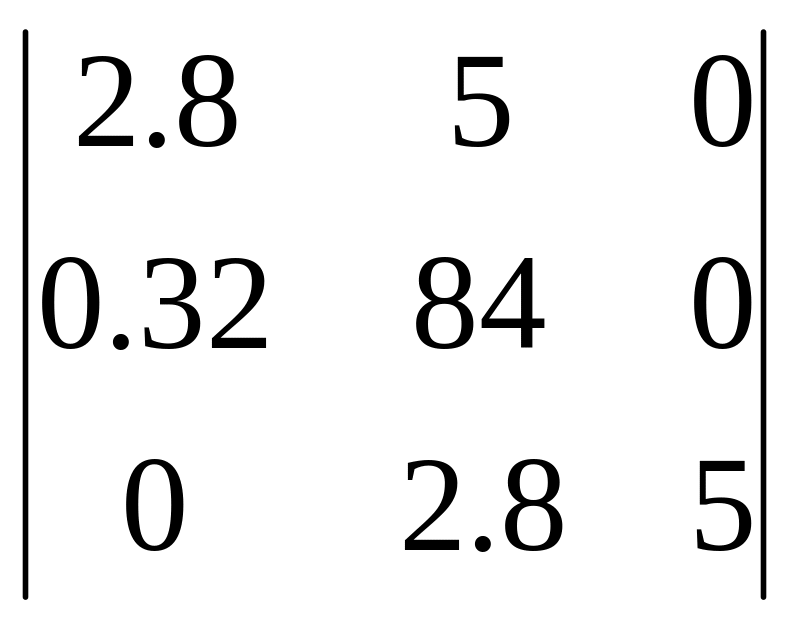Вычислим определители , , .

Система устойчива, т. к. все определители матрицы Гурвица положительны.

Из критерия Гурвица найдем критический коэффициент усиления, путем приравнения одного из определителей матрицы к нулю.

Получим: при , ;

при , ;

при , ;

2. 3. 3 Критерий Михайлова.

Согласно критерию Михайлова СРА устойчива, если годограф характеристического вектора, начинаясь с положительной оси, обходит последовательно в положительном направлении n квадрантов, где n=3 - порядок характеристического уравнения.

В характеристическом полиноме запишем коэффициент передачи в комплексной форме:

;

Построим годограф Михайлова:

;

;

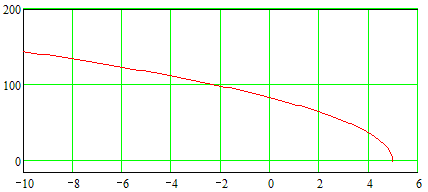
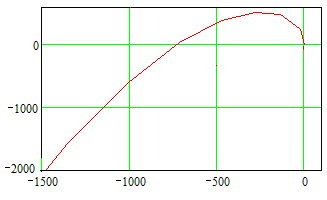
Рисунок 13. Годограф Михайлова.

Годограф данной системы удовлетворяет условию устойчивости, следовательно система устойчива.

2. 3. 4 Критерий Найквиста.

В передаточной функции разомкнутой системы запишем коэффициент передачи в комплексной форме:

;

Построим годограф Найквиста:

;

;

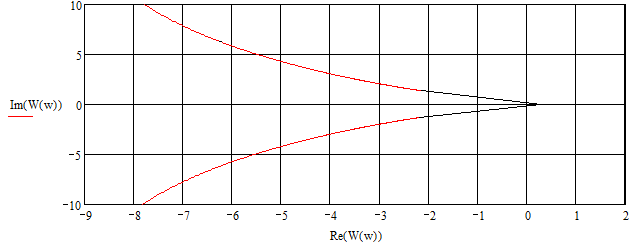
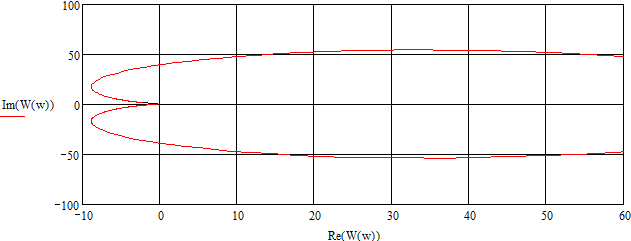
Рисунок 14. Годограф Найквиста.

Годограф не охватывает точку (-1;j0), следовательно система устойчива.

2. 3. 5 Оценка устойчивости по ЛЧХ.

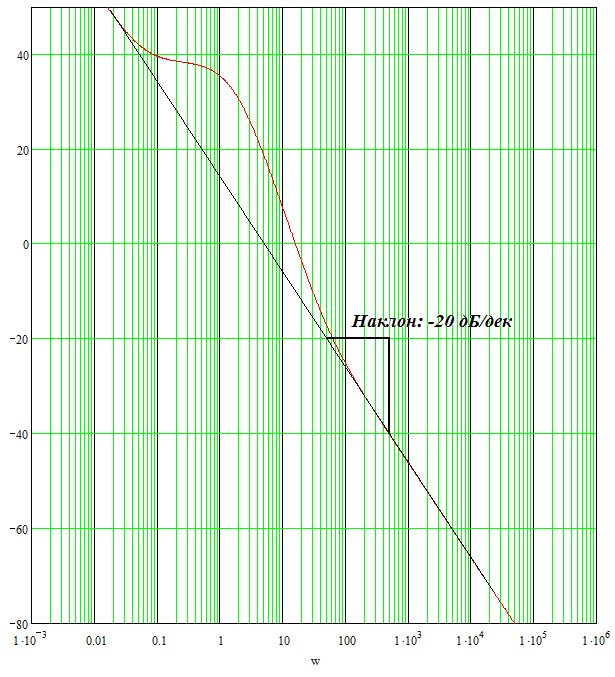
Рисунок 15. График ЛЧХ.

Из графика видно, что ЛЧХ пересекает ось частот под наклоном -20 (дБ/дек), следовательно условие выполняется, и система устойчивая.

2. 3. 6 Определение запаса устойчивости усилению и по фазе.

Определение запаса устойчивости усилению и по фазе разомкнутой системы.

Т. к. , то запас по усилению (амплитуде) .

Т. к. , то запас устойчивости по фазе .

Определение запаса устойчивости усилению и по фазе замкнутой системы.

Т. к. , то запас по усилению (амплитуде) .

Т. к. , то запас устойчивости по фазе .

2. 4 Передаточная функция замкнутой системы по ошибке.

Т.к. имеем О.О.С., то передаточная функция по ошибке будет находиться из выражения:

;

После подстановки H(p) в выше обозначенное выражение и упрощения получившегося, получим следующую передаточную функцию по ошибке:

;

Запишем передаточную функцию по ошибке в комплексной форме:

;

Модуль передаточной функции по ошибке будет иметь вид:

;

;

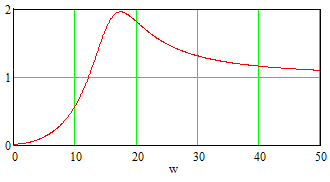
Рисунок 16. График передаточной функции замкнутой системы по ошибке.

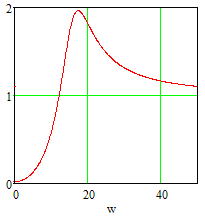
Рисунок 17. АЧХ замкнутой системы по ошибке.

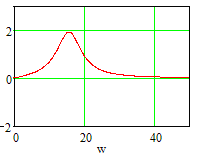
Рисунок 18. ФЧХ замкнутой системы по ошибке.