2.5.5 Група однакових і рівностоячих імпульсів (пачка імпульсів)
На самостійне опрацювання. Гоноровський ст.41-54.
Лекція№3. Подання сигналів з обмеженою смугою частот у вигляді ряду Котельникова
У теорії
і техніці сигналів широко використовується
теорема Котельникова (теорема відліків):
якщо найвища частота в спектрі функції
менше, ніж
,
то функція
повністю визначається послідовністю
значень у момент часу, віддалені один
від одного не більше ніж на
секунд.
Відповідно
до цієї теоремою сигнал
обмежений по спектру найвищої частотою
,
можна уявити рядом
(3.1)
У цьому
виразі
позначає
інтервал між двома відліковими точками
на осі часу, а
-
вибірка
функції
в момент часу
.
Вивчення функцій рядів ілюструє мал.3.10:
мал.3.1
функція виду
(3.2)
має такі властивості:
в точці
,
а в точках
,
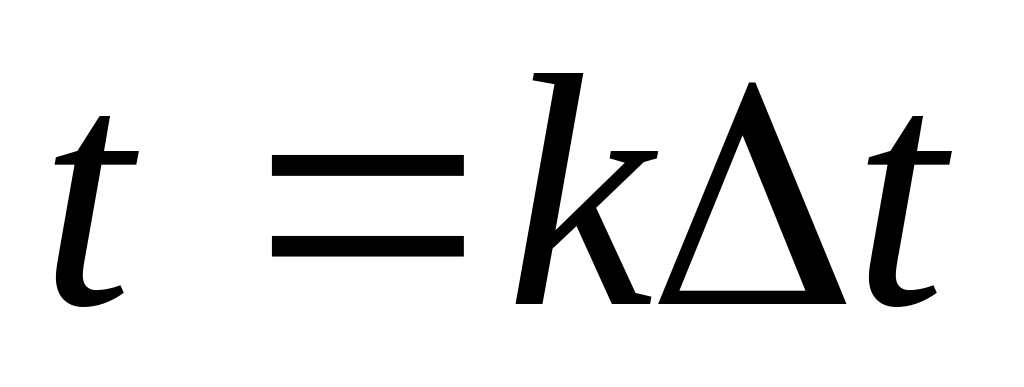де
-
будь-яке ціле позитивне чи негативне
число, відмінне від
спектральна щільність функції
рівномірна в смузі частот
і дорівнює
.
Так як
функція
відрізняється
від
тільки
зрушенням на осі часу на
,
то спектральна щільність функції
(3.3)
Ряд (3.1)
точно визначає заданий сигнал
в точках відліку, оскільки коефіцієнти
ряду є самі вибірки з функції, тобто
величини
.
Розглянемо
випадок коли тривалість сигналу
конечна і дорівнює
,
а смуга частот дорівнює
.
При цьому випадку і певних припущеннях
загальне число незалежних параметрів
(тобто значень
),
яка необхідна для повного завдання
сигналу, очевидно буде
При цьому виразі (3.1) приймає вигляд (при відліку часу від першої вибірки):
(3.4)
Число
іноді називають числом
степенів свободи
сигналу
,
а іноді і базою сигналу.
Енергію і середню потужність сигналу неважко виразити через задану послідовність тимчасових вибірок.
Середня
за час
потужність безперервного сигналу
дорівнює середньому квадрату вибірки,
число яких дорівнює
.
3.1 Дискретизовані сигнали
Дискретні сигнали виникають у тих випадках, коли джерело повідомлень видає інформацію у фіксовані моменти часу.
Дискретний
сигнал: його значення визначені лише в
рахунковому множині точок. Дискретний
сигнал
являє собою послідовність
відлікових значень сигналу
в точках
відповідно.
3.1.1 Дискретизована послідовність
На практиці,
відліки дискретних сигналів беруть у
часі через рівний проміжок
,
званий інтервалом
(кроком) дискретизації:
Операцію дискретизації, можна описати, вводячи в розгляд узагальнену функцію
звану дискретизованою послідовністю.
Дискретний
сигнал
являє собою функціонал, визначений на
множині всіляких аналогових сигналів
і рівний скалярному твору функцій
і
:
(3.5)
Формула (3.5) вказує шлях практичної реалізації пристрою для дискретного сигналу. Робота дискретизатора заснована на операції стробування - перемноження сигналу і гребінчатої функції (мал.3.2)
мал.3.2
3.1.2 Спектральна щільність дискретних сигналів
Дискретний сигнал з точністю до коефіцієнта пропорційності дорівнює добутку функції і дискретизуючій послідовності :
(3.6)
Відомо, що спектр твори двох сигналів пропорційний згортку їх спектральних густин. Тому якщо відомі закони відповідності сигналів і спектрів:
то спектральна щільність дискретизованого сигналу
(3.7)
Щоб знайти спектральну щільність дискретизуючої послідовності, розкладемо періодичну функцію в комплексний ряд Фур'є:
Коефіцієнти
цього ряду
Виходячи з фільтруючих властивостей дельта функції отримуємо
(3.8)
тобто
спектр дискретизуючої послідовності
складається з нескінченної сукупності
дельта-імпульсів у приватній області.
Дана спектральна щільність є періодичною
функцією з періодом
Підставимо формулу (3.8) в (3.7) і змінивши порядок проходження операцій інтегрування і підсумовування, знаходимо
(3.9)
Спектр
сигналу, отриманого в результаті
дискретизації нескінченно короткими
стробубчими імпульсами, являє собою
суму нескінченного числа "копій"
спектру вихідного аналогового сигналу.
Копії розташовуються на осі частот
через однакові інтервали
,
рівні значенням кутової частоти першої
гармоніки дискретизуючої імпульсної
послідовності.
мал.3.3