3.Ознака збіжності д’Аламбера.

Теорема 5. Якщо для додатного ряду існує границя 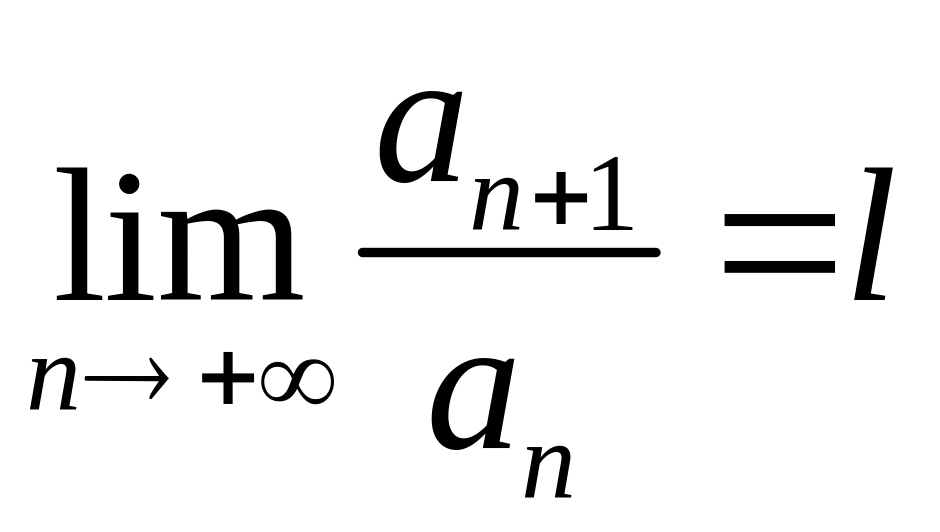, то ряд збігається при і розбігається при . При ряд може як збігатися,так і розбігатися.

Приклад 3.Дослідити на збіжність ряд (А-4) . Розв’язання ряд збігається за ознакою Д’Аламбера.

4. Знакозмінні ряди

Означеня 1. Знакозмінним називається ряд, злени якого по черзі мають то додатній то від’ємний знак:

₍₁₎

Означеня 2. Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд складений з модулей его членів ряд

(2)

Приклад1. Ряд збігається абсолютно, оскільки ряд збігається р=2>1.

Теорема 1. Ознака абсолютної збіжності. Нехай дан ряд (1).Якщо збігається ряд, який складається з модулей члені ряда (1), то ряд (1) також збігається.

Означеня 3. Ряд (1) може збігатися, хоч ряд з модулей ро збігається. Такі ряди називаються умовно збіжними.

4.1 Ознако Лейбниця збіжності знакозмінного ряда

Теорема 2. Якщо 1)члени знакозмінного ряда спадають по абсолютній величіні

2) –й член ряда прямує до нуля при

то ряд (1) збігається та його сума не більша 1-го члена

Наслідок. Залишок ряда (1) не більший першого члена, що відкидаєтся

Доведення. за означенням,

1.Якщо парне, то за теоремою 2.

2.Якщо непарне, то

Приклад 2 Обчислити суму ряда з точністю

Розв’язання. . подає суму ряда з точністю більшою 0.1.

47