3.3. Рента – строкова,

В фінансових контрактаж часто нарахування відсотків та надходження платежів співпадають у часі, тобто . Для одержання формули нарощеної суми скористаємось річною рентою з

. (3.1)

Різниця буде в тому, що тепер усі параметри характеризують ставку та платежі за період а не за рік. Тому змінюється на , – на , а кількість періодів буде добуток . Таким чином,. одержимо

(3.2)

Приклад 2.Розглянемо фінансовий контракт прикладу 1 за умовою , , тобто щомісяця в банк надходить 83.3гр. та щомісяця нараховуються відсотки зі ставкою

. За формулою (3.2) =100000(1.6453089-1)=64530.89(гр.).

Різниця нарощених сум з прикладу 2 та прикладу 1: =64531-61051=3480(гр.). Р-строкова рента дає більший прибуток, ніж річна на 3480гр.

Формули сучасної величини

3.4.Звичайна річна рента,

Сучасна величина потока платежів – це сума усіх його членів дисконтованих (зменшених) на величину відсоткової ставки на момент часу, співпадаючий з початком потоку платежів.

Погашення довгострокових кредитів. Нехай К – величина кредиту, виданного на n років, – щорічний внесок на погашення кредиту. Перший внесок виплачується по закінченні першого року і його дисконтна величина - , другий - по закінченні другого року і його дисконтна величина ,…, n-й внесок – наприкінці n-го року і його дисконтна величин .

Кредит буде погашено, коли

Сума в дужках - геометрична прогресія, де , , число членів

. (3.3)

Олержана формула для суми кредиту. З формули (3.3) випливає, що величина щорічного внеску для погашення кредиту та формула для обчислення строку ренти є такі:

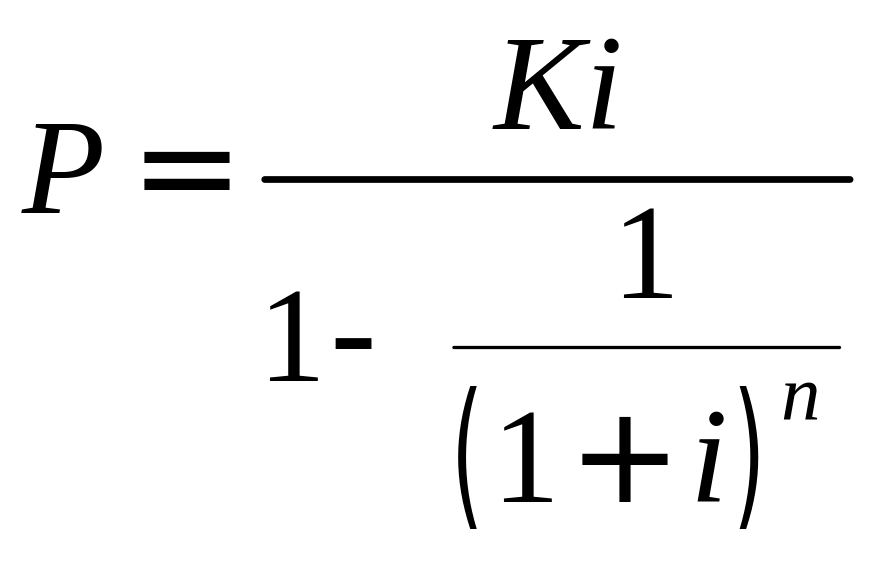(3. ) (3. )

Вираз називається коефіцієнтом погашення.

Приклад 3.Фірма планує узяти в банку кредит =5000000гр., і=0.05. Обчислити -суму щорічного внеску для погашення кредиту для :а) n=12 років; б) n=6 років та відсотки по кредиту.

Розв'язання. а) n=12 років. За формулою (3. ) .

б) n=6 років. За формулою (3. ) .

а) За 12 років відсотки по кредиту 12 Р–К=12 564127–5000000=1769524гр.

б) За 6 років відсотки по кредиту 6 Р–К=6 985087–5000000=910522гр. Різниця у відсотках: 1769524–910522=859002(гр.).Цей приклад планування природно підтверджує, що чим скоріше виплатиш кредит, тим менше сплатиш відсотків.

3.5. Рента – строкова,

Аналогічно формулі (3.3) можно одержати формулу сучасної вартості для – строкової ренти з

.

Основні формули для -строкових рент ( ) та їх наслідки

1.Нарощення. (Н_1), (Н_2), (Н_3)

2.Погашення. (П_1), (П_2), (П_3)

Розв'язання задач на основні формули

1.Батьки студента бажають покласти в банк, який виплачує 10% складних річних таку суму К , щоб їх син першокурсник міг знімати з цього рахунку кожний місяць 10000/p гр. та вичерпати увесь рахунок в кінці 6.5-річного ( разом з магістратурою) строку навчання. Яку суму мають покласти в банк батьки ст-та,якщо ?

Розв'язання. В цьому фінансовому контракті відбувається як-би “погашення кредиту”,наданого банку. =6.5 12=78 місяців. За формулою (П­­­_1)

=47654.63(гр.)

2.АТ створює благодійний фонд, вкладаючи в кінці кожного місяця внесок в банк в розмірі 40000/p гр.од. під складні 15% річних.Визначити розмір фонду :а)черз 5 років;б)через 10 років..

Розв'язання. а) .За формулою ( Н_1)

295248.4(гр.од.).

б) .

3.. Визначити, яку суму треба вкладати в банк щомісяця, щоб при ставці 8% складних річних через 5 років одержати 60000гр.од.

Розв'язання. а) .За формулою ( Н_2)

9799(гр.од.). В формулі ( Н_2) Р-щорічний внесок.Щомісячний внесок (гр.од.).

4..Протягом скількох років необхідно вкладати в кінці кожного місяця по 10000/p грн. при 11.5% скл-их річних, щоб одержати суму 60000 грн, якщо ?

Розв'язання. Оскільки треба знайти строк ренти при нарощенні, то за формулою ( Н_3)

4.58(року).

5.Протягом скількох років може бути погашена позика 40000 гр.,якщо сума щомісячного погашення 8000/p гр. при складній річній ставці 13.5%?

Розв'язання. Оскільки треба знайти строк ренти при погашенні, то скористаємось формулою

( П_3)

8.37року.

6..Для накопичення суми грошей під майбутні цілі в банк вкладається 3000гр. щомісяця, при річній ставці 8%. Яка сума буде отримана наприкінці 5-го року?

Розв'язання У формулі (3.2) та (Н_1) Р величина щорічного внеску, а в даному прикладі щомісячний внесок, тому застосовуємо наступну формулу