Деление многозначного числа на разрядное число.

Алгоритм деления на двузначные числа осуществляется в два приема. Сначала учащиеся учатся делить на круглые десятки и сотни. Учащиеся уже знакомы с приемами деления на 10, 100 и 1000,знают алгоритм деления на однозначное число. Таким образом, деление на круглые десятки и сотни должно быть сведено к последовательному делению на 10 (100) и однозначное число. Например, чтобы разделить 4560 на 50,достаточно разделить 4560 на 10, а затем 456 – на 5.

Для того, чтобы учащиеся могли сознательно использовать этот прием необходимо или показать , что деление числа на произведение можно выполнить различными способами.

a:(b*c)=(a:b):c = (a:c):b

Требовать заучивать правило не надо. Достаточно рассмотреть несколько задач допускающих практическое, хорошо иллюстрируемое решение. Например, «Отрезок длиной 12см разделить на 6 равных частей разными способами. Определить длину полученных частей». Учащиеся выполняют это задание тремя способами:

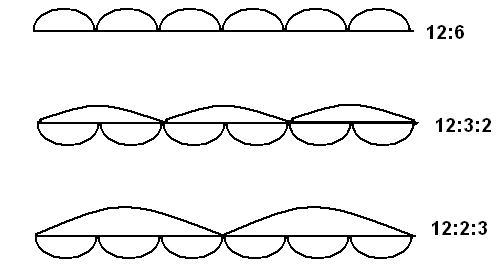
Затем переходят к изучению приема деления на круглые десятки и сотни.

Сначала рассмотрим частные, значения которых учащиеся находят устно: 210 : 70, 350 : 50, 562 : 40 и так далее

Учитель показывает как в данном случае может быть использован прием деления углом. Деление сопровождается пояснениями:

П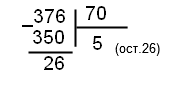 ервое неполное делимое 376. В частном будет одна цифра. Определим цифру частного: 376 : 10, получим 37. 37 разделим на 7 получим 5. Определим, сколько единиц делимого разделили: 70 * 5 = 350

Определи, сколько единиц делимого осталось: 376 – 350 = 26. Остаток меньше делителя – цифра частного подобрана верно.

Наконец, учащиеся переходят к делению множественных чисел на круглые десятки: 19889 : 70, 24810 : 30, 27540 : 60, 42150 : 50 и так далее.

У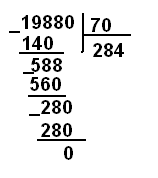 читывая сложность этих случав, запоминают промежуточные операции. Операция подбора цифр частного подробно поясняется. Например, «первое неполное делимое 198. В частном будет 3 цифры. Определим первую цифру частного: 198 разделим на 10, получим 19; 19 разделим на 7 получаем 3. Запоминаем 2 в частное. Выясним, сколько единиц неполного делимого разделили: 70 * 2 = 140.

Определим, сколько единиц неполного делимого осталось 198 – 140 = 58. Остаток меньше делителя, значит, цифра частного подобрана верно. Определим следующее неполное делимое….» и так далее.

Методика изучения деления числа на круглые сотни аналогична.

Сначала рассмотрим случаи, когда результат может быть вычислен устно: 4200 : 700, 56000 : 800,120000 : 300 и так далее. Используется прием: 4200 : 700 = 4200 : 100 : 7 = 42 : 7 = 6

В более сложных случаях значение частного находится углом: «Первое неполное делимое 6785. В частном 1 цифра. Определим цифру частного: 6785 разделим на 100, получаем 67, 67 разделим на 8, получаем 8. В частном записываем 8. Вычислим, сколько единиц неполного делимого разделили: 800 * 8 = 6400. Определим, сколько единиц еще осталось разделить 6785 – 6400 = 385. Остаток меньше делителя, значит цифра частного подобрана верно».

Н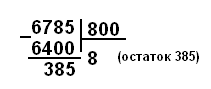 аконец, выполняется деление многозначных чисел на круглые сотни: 136500 : 500, 246300 : 300, 658400 : 800 и так далее.

Работа над приемами деления на круглые десятки и сотни может проводиться параллельно .