16Ложные корреляции. Причины и пути решения проблем.

Ложные корреляции. По коэффициентам корреляции нельзя строго доказать причинной зависимости между переменными. Однако можно определить ложные корреляции, т.е. корреляции, которые обусловлены влияниями «других», остающихся вне поля зрения исследователя, переменных (которые влияют на коррелируемые переменные). При «контролировании» (исключении) этих переменных исходная корреляция либо исчезнет, либо, возможно, даже изменит свой знак. Основная проблема ложной корреляции состоит в том, что исследователь не знает, кто является ее «агентом». Тем не менее, исследователь может воспользоваться частными корреляциями, чтобы контролировать (частично исключая) влияние определенных переменных.

17Уравнение регресии. Основные этапы построения уравнения. Методы статестического оценивания правильности построения уравнения.

Основа регрессионного анализа заключается в том, чтобы найти кривую, наиболее близко проходящую по всем точкам разброса.

Любую кривую можно выровнять в прямую

F(x) = a0 + a1x –уравнение прямой

(разброс точек одинаков относительно кривой) Если нет, то проблема гетероследов(???)

Точка первична(?) – найти производную Сумма всех возможных отклонений должна стремиться к минимуму.

t2 – коэффициент Стьюдента при α=0,05, t2 = 2,306 (табличное значение)

Когда строим, существует 2 ошибки:1.ошибка модели2.ошибка выборочной совокупности

Чтобы снять вторую ошибку, формулу уточняют

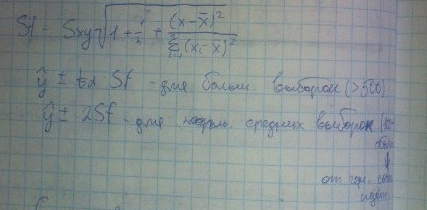
Степень влияния х на у (оценка):Для этого исслед-м:

Правило сложения дисперсий (Анова)

Общая дисперсия-дисперсия у.

Вариация упод воздействием все факторов.

Дисперсия вычисляется по формуле для 2 видов данных: сгруппированных и несгруппированных

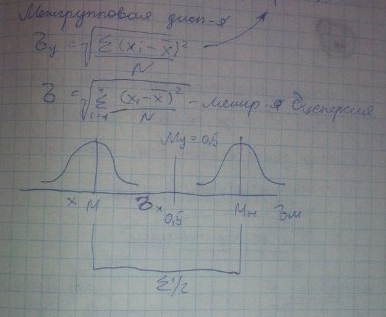
«Выбросы» ведут к ослаблению связи. Нужно понять сколько их.

Межгрупповая дисперсия: среднее по группам минус средняя межгрупповая, деленная на количество групп.

Внутригрупповая дисперсия – это вариации упод воздействием неучитываемых факторов (дисперсия ошибки)

Для принимаемой модели( выделенные):1Коэффициент детерминации (для всей модели)2Коэффициент Стьюдента (для коэффициентов а1 и а0) 3Коэффициент Фишера (длявсе модели)4Анализ остатков

18Коэффициент детерминации. Логика построения и интерпритация показателя. Дисперсионный анализ.

Коэффициент детерминации (  - R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости, то есть объясняющими переменными. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по факторам дисперсии зависимой переменной) в дисперсии зависимой переменной. Его рассматривают как универсальную меру связи одной случайной величины от множества других. В частном случае линейной зависимости   является квадратом так называемого множественного коэффициента корреляции между зависимой переменной и объясняющими переменными. В частности, для модели парной линейной регрессии коэффициент детерминации равен квадрату обычного коэффициента корреляции между y и x.

Истинный коэффициент детерминации модели зависимости случайной величины y от факторов x определяется следующим образом:

где   — условная (по факторам x) дисперсия зависимой переменной или дисперсия случайной ошибки модели.

В данном определении используются истинные параметры, характеризующие распределение случайных величин. Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):

где  -сумма квадратов остатков регрессии,   - фактические и расчетные значения объясняемой переменной.

 - общая сумма квадратов.

В случае линейной регрессии с константой  , где   — объяснённая сумма квадратов, поэтому получаем более простое определение в этом случае — коэффициент детерминации — это доля объяснённой суммы квадратов в общей:

Необходимо подчеркнуть, что эта формула справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.

Интерпретация:

1. Коэффициент детерминации для модели с константой принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50% (в этом случае коэффициент множественной корреляции превышает по модулю 70%). Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими (коэффициент корреляции превышает 90%). Значение коэффициента детерминации 1 означает функциональную зависимость между переменными.

2. При отсутствии статистической связи между объясняемой переменной и факторами, статистика   для линейной регрессии имеет асимптотическое распределение  , где   — количество факторов модели (см. тест множителей Лагранжа). В случае линейной регрессии с нормально распределёнными случайными ошибками статистика   имеет точное (для выборок любого объёма) распределение Фишера   (см. F-тест). Информация о распределении этих величин позволяет проверить статистическую значимость регрессионной модели исходя из значения коэффициента детерминации. Фактически в этих тестах проверяется гипотеза о равенстве истинного коэффициента детерминации нулю.

Дисперсионный анализ применяют для изучения влияния качественных признаков на количественную переменную. Например, пусть имеются k выборок результатов измерений количественного показателя качества единиц продукции, выпущенных на k станках, т.е. набор чисел (x₁(j), x₂(j), … , x_n(j)), где j – номер станка, j = 1, 2, …, k, а n – объем выборки. В распространенной постановке дисперсионного анализа предполагают, что результаты измерений независимы и в каждой выборке имеют нормальное распределение N(m(j), σ²) с одной и той же дисперсией. Хорошо разработаны и непараметрические постановки.

Проверка однородности качества продукции, т.е. отсутствия влияния номера станка на качество продукции, сводится к проверке гипотезы

H₀: m(1) = m(2) = … = m(k).

В дисперсионном анализе разработаны методы проверки подобных гипотез. Теория дисперсионного анализа и расчетные формулы рассмотрены в специальной литературе.

Гипотезу Н₀ проверяют против альтернативной гипотезы Н₁, согласно которой хотя бы одно из указанных равенств не выполнено. Проверка этой гипотезы основана на следующем «разложении дисперсий», указанном Р.А.Фишером:

   (7)

где s² – выборочная дисперсия в объединенной выборке, т.е.

Далее, s²(j) – выборочная дисперсия в j-ой группе,

Таким образом, первое слагаемое в правой части формулы (7) отражает внутригрупповую дисперсию. Наконец,   - межгрупповая дисперсия,

Область прикладной статистики, связанную с разложениями дисперсии типа формулы, называют дисперсионным анализом. В качестве примера задачи дисперсионного анализа рассмотрим проверку приведенной выше гипотезы Н₀в предположении, что результаты измерений независимы и в каждой выборке имеют нормальное распределение N(m(j), σ²) с одной и той же дисперсией. При справедливости Н₀ первое слагаемое в правой части формулы (7), деленное на σ², имеет распределение хи-квадрат с k(n-1) степенями свободы, а второе слагаемое, деленное на σ², также имеет распределение хи-квадрат, но с (k-1) степенями свободы, причем первое и второе слагаемые независимы как случайные величины. Поэтому случайная величина

имеет распределение Фишера с (k-1) степенями свободы числителя и k(n-1) степенями свободы знаменателя. Гипотеза Н₀ принимается, если F < F_1-α, и отвергается в противном случае, где F_1-α – квантиль порядка 1-α распределения Фишера с указанными числами степеней свободы.  Такой выбор критической области определяется тем, что при Н₁ величина F безгранично увеличивается при росте объема выборок n. Значения F_1-α берут из соответствующих таблиц.

Разработаны непараметрические методы решения классических задач дисперсионного анализа, в частности, проверки гипотезы Н₀.