
- •1Две стратегии исследования (восходящая и нисходящая). Привести примеры.
- •2Роль и место моделирования объекта в социологическом исследовании
- •3Понятие модель (3 значения понятия). Привести пример
- •4Виды моделей. Их характеристики. Виды когнитивных моделей. Привести пример когнитивной модели
- •5Способы построения операциональных моделей. Типы шкал. Способы перевода данных их одной шкалы в другую.
- •Вопрос 5.Построение операцмодели.Шкалы
- •6Показатели и индексы. Типология показателей.
- •6Показатели и индексы. Типология показателей.
- •Примерная типология показателей, используемых для построения исходной модели социального объекта
- •7Индексы динамических рядов. Принцип их построения.
- •8Индексы структурных сдвигов. Принцип их построения.
- •9Факторный индексный анализ. Принцип осуществления.
- •Измерение влияния факторов в индексном анализе
- •Данные для факторного анализа объема валовой продукции
- •10 Типы математических моделей. Основные статистические способы построение разных типов моделей (классификация методов)
- •11Этапы построения базисной модели для прогнозирования и модели прогнозного фона.
- •12Поисковый прогноз. Этапы осуществления поискового прогноза
- •13Нормативный прогноз. Этапы осуществления нормативного прогноза
- •14Способы задания нормативов. Какими методами можно построить каждый норматив.
- •15Корреляционный анализ. Тип связей. Коэффициенты корреляций. Условия их применения. Интерпритация показателей связи.
- •Определение
- •Условия применения и ограничения корреляционно-регрессионного метода
- •16Ложные корреляции. Причины и пути решения проблем.
- •17Уравнение регресии. Основные этапы построения уравнения. Методы статестического оценивания правильности построения уравнения.
- •18Коэффициент детерминации. Логика построения и интерпритация показателя. Дисперсионный анализ.
- •19Какие проблемы (ошибки расчета) содержит метод экспертного оценивания. Методы предотвращения ошибок оценивания.
- •20Методы определения гомогенности экспертов.
- •21Этапы проведения экспертного оценивания.
- •Постановка цели исследования
- •Выбор формы исследования, определение бюджета проекта
- •Подготовка информационных материалов
- •Подбор экспертов
- •Проведение экспертизы
- •Статистический анализ результатов
- •22 Правильность построения модели (верификация прогноза)
Определение
Заданы
две выборки
![]() .
.
Вычисление корреляции Спирмена:
Коэффициент корреляции Спирмена вычисляется по формуле:
![]() ,
где
,
где
![]() -
ранг наблюдения
-
ранг наблюдения
![]() в
ряду
в
ряду
![]() ,
,
![]() -
ранг наблюдения
-
ранг наблюдения
![]() в
ряду
в
ряду
![]() .
.
Коэффициент
![]() принимает
значения из отрезка
принимает
значения из отрезка
![]() .
Равенство
.
Равенство
![]() указывает
на строгую прямую линейную зависимость,
указывает
на строгую прямую линейную зависимость,
![]() на
обратную.
на
обратную.
Коэффициент корреляции Пирсона характеризует существование линейной зависимости между двумя величинами.
Пусть
даны две выборки
![]() коэффициент
корреляции Пирсона рассчитывается по
формуле:
коэффициент
корреляции Пирсона рассчитывается по
формуле:
где
![]() –
выборочные средние
–
выборочные средние
![]() и
и
![]() ,
,
![]() –
выборочные дисперсии,
–
выборочные дисперсии,
![]() .
.
Коэффициент корреляции Пирсона называют также теснотой линейной связи:
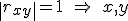 линейно
зависимы,
линейно
зависимы,
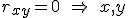 линейно
независимы.
линейно
независимы.
Коэффициент корреляции Кенделла (Kendall tau rank correlation coefficient) — мера линейной связи между случайными величинами. Корреляция Кенделла является ранговой, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги. Коэффициент инвариантен по отношению к любому монотонному преобразованию шкалы измерения.
Заданы
две выборки
![]() .
.
Вычисление корреляции Кенделла:
Коэффициент корреляции Кенделла вычисляется по формуле:
![]() ,
где
,
где
![]() —
количество инверсий, образованных
величинами
,
расположенными в порядке возрастания
соответствующих
.
—
количество инверсий, образованных
величинами
,
расположенными в порядке возрастания
соответствующих
.
Коэффициент
![]() принимает
значения из отрезка
.
Равенство
принимает
значения из отрезка
.
Равенство
![]() указывает
на строгую прямую линейную зависимость,
указывает
на строгую прямую линейную зависимость,
![]() на
обратную.
на
обратную.
Условия применения и ограничения корреляционно-регрессионного метода
Поскольку корреляционная связь является статистической, первым условием возможности ее изучения является наличие данных по достаточно большой совокупности. По отдельным явлениям можно получить совершенно превратное представление о связи признаков, ибо в каждом отдельном явлении значения признаков, кроме закономерной составляющей, имеют случайное отклонение (вариацию). Например, сравнивая два хозяйства, одно из которых имеет лучшее качество почв, по уровню урожайности, можно обнаружить, что урожайность выше в хозяйстве с худшими почвами. Ведь урожайность зависит от сотен факторов и при том же самом качестве почв может быть и выше, и ниже. Но если сравнивать большое число хозяйств с лучшими почвами и большое число — с худшими, то средняя урожайность в первой группе окажется выше и станет возможным измерить достаточно точно параметры корреляционной связи.
Вторым условием закономерного проявления корреляционной связи служит условие, обеспечивающее надежное выражение закономерности в средней величине. Кроме уже указанного большого числа единиц совокупности для этого необходима достаточная однородность совокупности. Нарушение этого условия может извратить параметры корреляции. Например, в массе зерновых хозяйств уровень продукции с 1 га растет по мере концентрации площадей, т.е. он выше в крупных хозяйствах. В массе овощных и овощемолочных хозяйств (пригородный тип) наблюдается та же прямая связь уровня продукции с размером хозяйства. Но если соединить в общую неоднородную совокупность те и другие хозяйства, то связь уровня продукции с размером площади пашни (или посевной площади) получится обратной. Причина в том, что овощные и овощемолочные хозяйства, имея меньшую площадь, чем зерновые, производят больше продукции с 1 га ввиду большей интенсивности производства в данных отраслях.
В качестве третьего условия корреляционного анализа выдвигается необходимость подчинения распределения совокупности по результативному и факторным признакам нормальному закону распределения вероятностей. Это условие связано с применением метода наименьших квадратов при расчете параметров корреляции: только при нормальном распределении метод наименьших квадратов дает оценки параметров, отвечающих принципам максимального правдоподобия.
