14Способы задания нормативов. Какими методами можно построить каждый норматив.

1)Ценностный А) есть идеал (что-то мифическое) Б) эталон (лучший среди других) Например, выборы. Люди хотят идеальное государство. Метод. Регрессия (такая вот прямая, это я так думаю, нефакт)

2) Проблемный способ 3) Cитуационно-нормативный -высчитываем среднее среди других объектов (в медицине) -взять среднее из лучшей группы -использование теории оптимизации – имеем некоторые эффективные объекты, определяем факторы, от которых зависит эффективное состояние (в педагогике, где определяем уровень ученика, тесты)

15Корреляционный анализ. Тип связей. Коэффициенты корреляций. Условия их применения. Интерпритация показателей связи.

Корреляционная связь — это согласованное изме­нение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью дру­гого.

Оба термина, корреляционная связь и корреляционная зависимость — часто используются как синони­мы. Зависимость подразумевает влияние, связь — любые согласован­ные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого.

Корреляционная зависимость -  это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака.

Корреляционные связи различаются по форме, направлению и степени (силе).

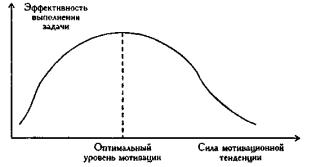
По форме корреляционная связь может быть прямолинейной или криволинейной. Прямолинейной может быть, например, связь между количеством тренировок на тренажере и количеством правильно решае­мых задач в контрольной сессии. Криволинейной может быть, напри­мер, связь между уровнем мотивации и эффективностью выполнения задачи (см. рис. 1). При повышении мотивации эффективность вы­полнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффективность выполнения задачи; дальнейшему повышению мотивации сопутст­вует уже снижение эффективности.

По направлению корреляционная связь может быть положитель­ной ("прямой") и отрицательной ("обратной"). При положительной прямолинейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значе­ниям одного признака - низкие значения другого. При отрицательной корреляции соотношения обратные. При положительной корреляции коэффициент корреляции имеет положительный знак, например r=+0,207, при отрицательной корреля­ции - отрицательный знак, например r=—0,207.

Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции.

Максимальное воз­можное абсолютное значение коэффициента корреляции r=1,00; минимальное r=0,00.

Таблица 3. Использование коэффициента корреляции в зависимости от типа переменных

Тип шкалы		Мера связи
Переменная X	Переменная У
Интервальная или отношений	Интервальная или отношений	Коэффициент Пирсона
Ранговая, интервальная или отношений	Ранговая, интервальная или отношений	Коэффициент Спирмена
Ранговая	Ранговая	Коэффициент Кендалла
Дихотомическая	Дихотомическая	Коэффициент «»
Дихотомическая	Ранговая	Рангово-бисериальный
Дихотомическая	Интервальная или отношений	Бисериальный

Коэффициент корреляции Пирсона

Коэффициент характеризует наличие только линейной свя­зи между признаками, обозначаемыми, как правило, символами X и Y. Формула расчета коэффициента корреляции построена таким образом, что, если связь между признаками имеет ли­нейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициен­том линейной корреляции Пирсона. Если же связь между пере­менными X и Y не линейна, то Пирсон предложил для оценки тесноты этой связи так называемое корреляционное отношение.

Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 — являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно произошла ошибка в вычислениях.

Если знак ко­эффициента линейной корреляции — плюс, то связь между кор­релирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина дру­гого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно уве­личивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости.

При наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой пере­менной. Такая зависимость носит название обратно пропорцио­нальной зависимости.

В общем виде формула для подсчета коэффициента корреля­ции такова:

                       где  х_i — значения, принимаемые в выборке X, y_i — значения, принимаемые в выборке Y;  — средняя по X,  — средняя по Y.

Расчет коэффициента корреляции Пирсона предполагает, что переменные Х и У распределены нормально.

Типы связей.

Для описания причинно-следственной связи между явлениями и процессами используется деление статистических признаков, отражающих отдельные стороны взаимосвязанных явлений, на факторные и результативные. Факторными считаются признаки, обуславливающие изменение других, связанных с ними признаков, являющихся причинами и условиями таких изменений. Результативными являются признаки, изменяющимися под воздействием факторных.

Формы проявления существующих взаимосвязей весьма разнообразны. В качестве самых общих их видов выделяют функциональную и статистическую связи.

Функциональной называют такую связь, при которой определённому значению факторного признака соответствует одно и только одно значение результативного. Такая связь возможна при условии, что на поведение одного признака (результативного) влияет только второй признак (факторный) и никакие другие. Такие связи являются абстракциями, в реальной жизни они встречаются редко, но находят широкое применение в точных науках и в первую очередь, в математике. Например: зависимость площади круга от радиуса: S=π∙r2

Функциональная связь проявляется во всех случаях наблюдения и для каждой конкретной единицы изучаемой совокупности. В массовых явлениях проявляются статистические связи, при которых строго определённому значению факторного признака ставится в соответствие множество значений результативного. Такие связи имеют место, если на результативный признак действуют несколько факторных, а для описания связи используется один или несколько определяющих (учтённых) факторов.

Примером статистической связи может служить зависимость себестоимости единицы продукции от уровня производительности труда: чем выше производительность труда, тем ниже себестоимость.

Корреляционная связь проявляется только на всей статистической совокупности, а не в каждом отдельном случае, так как только при достаточно большом числе случаев каждому случайному значению факторного признака будет соответствовать распределение средних значений случайного признака y.

По направлению корреляционные связи делятся на прямые и обратные. При прямой связи результативный признак растёт с увеличением факторного, при обратной - рост факторного признака приводит к снижению значений результативного признака. Например, чем больше стаж работы, тем выше производительность труда – прямая связь, а чем выше производительность труда, тем ниже себестоимость единицы продукции – обратная связь.

По форме (аналитическому выражению) связи делятся на линейные (прямолинейные) и нелинейные (криволинейные) связи. Линейные связи выражаются уравнением прямой, а нелинейные – уравнением параболы, гиперболы, степенной и т. п.

По количеству взаимодействующих факторов связи делятся на парную (однофакторную) и множественную (многофакторную) связи. При парной связи на результативный признак действует один факторный, при множественной – несколько факторных признаков. Исследование статистической связи проводится в следующем порядке:􀂃 качественный анализ связи - определение состава признаков, предварительный анализ формы связи;􀂃 сбор данных на основе статистического наблюдения;􀂃 количественная оценка тесноты связи по эмпирическим данным;􀂃 регрессионный анализ (аналитическое описание связи):

- выбор формы связи,

- оценка параметров модели,

- оценка качества модели

Коэффициент корреляции.

Вводится коэффициент корреляции. Он рассчитывается следующим образом:

Есть массив из n точек {x_1,i, _x2,i}

Рассчитываются средние значения для каждого параметра:

И коэффициент корреляции:

r изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x₁ и x₂: r равен 1 (или -1), если связь линейна.

Коэффициент r является случайной величиной, поскольку вычисляется из случайных величин. Для него можно выдвигать и проверять следующие гипотезы:

Коэффициент корреляции Спирмена (Spearman rank correlation coefficient) — мера линейной связи между случайными величинами. Корреляция Спирмена является ранговой, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги. Коэффициент инвариантен по отношению к любому монотонному преобразованию шкалы измерения.