2. Методом Гаусса-Зейделя решим ту же самую, которую решили методом Якоби:
Система приведенная к нормальному виду:
В
качестве начального приближения возьмем
нулевой вектор свободных членов
:
; ;
Применяя процесс Зейделя, последовательно получим:
и т.д.
После новой подстановки будем иметь третьи приближения корней:
;
;
Решение не сходится до точности =0,1, наша система расходится.
|
Метод Гаусса-Зейделя |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
к |
х1 |
х2 |
х3 |
х1(к)-x1(к-1) |
х2(к)-x2(к-1) |
х3(к)-x3(к-1) |
max |
||||||
0 |
0,00 |
0,00 |
0,00 |
|
|
|
|
||||||
1 |
2,67 |
0,36 |
-7,24 |
2,67 |
0,36 |
7,24 |
7,24 |
||||||
2 |
-28,96 |
2,55 |
78,35 |
31,63 |
2,20 |
85,59 |
85,59 |
||||||
3 |
325,63 |
-21,66 |
-880,85 |
354,59 |
24,21 |
959,20 |
959,20 |
||||||
4 |
-3649,55 |
249,78 |
9872,28 |
3975,18 |
271,44 |
10753,13 |
10753,13 |
||||||
5 |
40914,34 |
-2793,19 |
-110676,02 |
44563,89 |
3042,97 |
120548,30 |
120548,30 |
||||||
6 |
-458670,60 |
31320,11 |
1240734,69 |
499584,94 |
34113,30 |
1351410,72 |
1351410,72 |
||||||
7 |
5141942,73 |
-351108,12 |
########## |
5600613,33 |
382428,24 |
15150034,09 |
15150034,09 |
||||||
Проверяем условие сходимости итерационного процесса:
Три нормы матриц нормальной системы имеют больше единицы, то итерационный процесс не сходится к единственному решению.
3. Преобразуем нашу систему до сходимости итерационного процесса. Приведем систему к виду, годному для применения итерационных методов решения:
В уравнении (С) коэффициент при х1 по модулю больше суммы модулей остальных коэффициентов. Делаем перестановку системы уравнений, уравнение (С) переставим в уравнение (А). В итоге получаем преобразованную систему линейных уравнений, эквивалентную исходной,
,
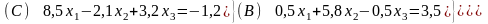и удовлетворяющую условиям сходимости итерационного процесса
После преобразовании получим систему при методе Якоби:
-
Метод Якоби для решения СЛАУ
Исходные данные
Матрица
х1
х2
х3
0
0,25
-0,38
-0,14
e=0,1
-0,09
0
0,09
0,6
0,24
0,71
0
-0,63
к
х1
х2
х3
х1(к)-x1(к-1)
х2(к)-x2(к-1)
х3(к)-x3(к-1)
max
0
0,00
0,00
0,00
1
-0,14
0,60
-0,63
0,14
0,60
0,63
0,63
2
0,25
0,56
-0,24
0,39
0,04
0,39
0,39
3
0,09
0,56
-0,18
0,16
0,00
0,06
0,16
4
0,07
0,58
-0,21
0,02
0,02
0,04
0,04
5
0,09
0,57
-0,21
0,02
0,00
0,01
0,02
6
0,08
0,57
-0,20
0,00
0,00
0,00
0,00
7
0,08
0,57
-0,20
0,00
0,00
0,00
0,00
8
0,08
0,57
-0,20
0,00
0,00
0,00
0,00
При методе Гаусса-Зейделя:
|
Метод Гаусса-Зейделя для решения СЛАУ |
|
|
|
|
|
|||||||
|
|
Исходные данные |
|
|
|
|
|
||||||
|
|
Матрица |
|
|
|
|
|
|
|||||
|
х1 |
х2 |
х3 |
|
|
|
|
||||||
|
0 |
0,25 |
-0,38 |
-0,14 |
|
e=0,1 |
|
|
|||||
|
-0,09 |
0 |
0,09 |
0,6 |
|
|
|
|
|||||
|
0,24 |
0,71 |
0 |
-0,63 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
к |
х1 |
х2 |
х3 |
х1(к)-x1(к-1) |
х2(к)-x2(к-1) |
х3(к)-x3(к-1) |
max |
||||||
0 |
0,00 |
0,00 |
0,00 |
|
|
|
|
||||||
1 |
-0,14 |
0,61 |
-0,23 |
0,14 |
0,61 |
0,23 |
0,61 |
||||||
2 |
0,10 |
0,57 |
-0,20 |
0,24 |
0,04 |
0,03 |
0,24 |
||||||
3 |
0,08 |
0,57 |
-0,20 |
0,02 |
0,00 |
0,00 |
0,02 |
||||||
4 |
0,08 |
0,57 |
-0,20 |
0,00 |
0,00 |
0,00 |
0,00 |
||||||
5 |
0,08 |
0,57 |
-0,20 |
0,00 |
0,00 |
0,00 |
0,00 |
||||||
6 |
0,08 |
0,57 |
-0,20 |
0,00 |
0,00 |
0,00 |
0,00 |
||||||
7 |
0,08 |
0,57 |
-0,20 |
0,00 |
0,00 |
0,00 |
0,00 |
||||||
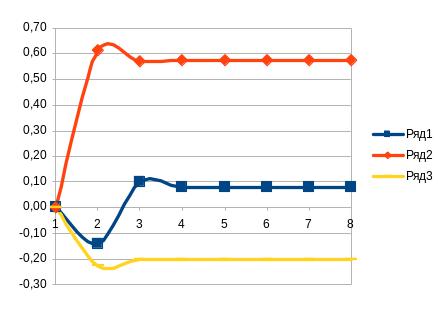
Контрольная работа №3