Пермский государственный технический университет

Строительный факультет

Кафедра строительной механики и вычислительной техники

Контрольные задания №1,2,3,4,5

(по курсу «Численные методы»)

Вариант26

Выполнил:

Студент гр. ПГСз-10-1

Новикова И.О.

Проверил:

Кашеварова

Пермь 2012

Контрольная работа №1

Тема: Численные методы решения задач линейной алгебры,

метод Гаусса

1. Методом Гаусса решим систему уравнений:

Решим эту систему в матричной форме:

AX=B,

где А — матрица системы, Х — вектор решения, В — вектор свободных членов.

Составим матрицу коэффициентов, включая свободные члены (расширенную матрицу):

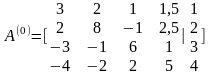
2. Прямой ход:

Шаг 1. 1-ую строку матрицы делим на а₁₁=3, умножаем полученную строку сначала на а₂₁ (-2) и складываем со 2-ой, затем на а₃₁ (3) и складываем с 3-ей, после на а₄₁ (4) и складываем с 4-ой:

Шаг 2. 2-ую строку матрицы А⁽¹⁾ делим на а₂₂=6,67, умножаем полученную строку на а₃₂ (-1) и складываем с 3-ей, затем на а₄₂ (0,67) и складываем с 4-ой:

Шаг 3. 3-ю строку матрицы А⁽²⁾ делим на а₃₃=7,25, умножаем полученную строку на а₄₃ (3,5) и складываем с 4-ой:

Обратный ход:

Из последнего уравнения (4-ая строка матрицы) получаем:

Из 3-его уравнения находим

Из 2-ого уравнения находим

Из 1-ого уравнения получаем

Таким образом, полученное решение имеет вид

Решим этот пример с использованием электронных таблиц Excel и получим такой вид:

Метод Гаусса		Прямой ход						Обратный ход
	Матрица А				B		x1=	-0,1751
3	2		1	1,5	1		x2=	0,1535
2	8		-1	2,5	2		x3=	0,3405
-3	-1		6	1	3		x4=	0,5851
-4	-2		2	5	4
	1-ый шаг
1,00	0,67		0,33	0,50	0,33
0,00	6,67		-1,67	1,50	1,33
0,00	1,00		7,00	2,50	4,00
0,00	0,67		3,33	7,00	5,33
	2-ой шаг
1,00	0,67		0,33	0,50	0,33
0,00	1,00		-0,25	0,23	0,20
0,00	0,00		7,25	2,28	3,80
0,00	0,00		3,50	6,85	5,20
	3-ий шаг
1,00	0,67		0,33	0,50	0,33
0,00	1,00		-0,25	0,23	0,20
0,00	0,00		1,00	0,31	0,52
0,00	0,00		0,00	5,75	3,37

3. Система имеет единственное решение, если матрица А является невырожденной (detA0), т.е detА=1115,757,256,673=834,17.

4. Матрица А^-1 называется обратной по отношению к данной матрице А и находится из условия АА^-1=А^-1А=Е

Пусть имеем невырожденную матрицу А:

Тогда

; ; ; ;

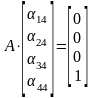Приводя матрицу коэффициентов к треугольному виду и выполняя обратный ход для каждой системы, получаем:

1. 

;

2. 

;

3. 

;

4. 

;

5. Величина называется нормой матрицы А=а_ij и определяется по одной из 3-х формул:

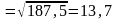
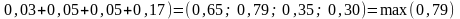
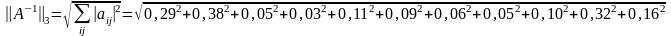
6. Определяем меру обусловленности

Число обусловленности является мерой чувствительности системы линейных алгебраических уравнений A·В=Х, определяемой матрицей коэффициентов А, к погрешностям вектора В правых частей уравнений. Чем больше число обусловленности, тем более неустойчив процесс решения системы. В нашем примере, матрица А и матрица АА^-1, хорошо обусловленная.

7. Решим этот пример при возмущении 0,1 с использованием электронных таблиц Excel и получим вид:

	Матрица А			B			Обратный ход
3,1	2,1	1,1	1,6	1,1		x1=	-0,1798
2,1	8,1	-1,1	2,6	2,1		x2=	0,1638
-3,1	-1,1	6,1	1,1	3,1		x3=	0,3406
-4,1	-2,1	2,1	5,1	4,1		x4=	0,5866
	1-ый шаг
1,00	0,68	0,35	0,52	0,35
0,00	6,68	-1,85	1,52	1,35
0,00	1,00	7,20	2,70	4,20
0,00	0,68	3,55	7,22	5,55
	2-ой шаг
1,00	0,68	0,35	0,52	0,35
0,00	1,00	-0,28	0,23	0,20
0,00	0,00	7,48	2,47	4,00
0,00	0,00	3,74	7,06	5,42
	3-ий шаг
1,00	0,68	0,35	0,52	0,35
0,00	1,00	-0,28	0,23	0,20
0,00	0,00	1,00	0,33	0,53
0,00	0,00	0,00	5,82	3,42

Оценим относительную погрешность решения

при 0,1

Получаем

Таким образом, система уравнений является хорошо обусловленной, а ее решение устойчивым, т.к. мера обусловленности detA невелика и матрица А хорошо обусловлена.

Контрольная работа №2