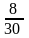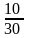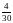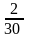Вариант 20

1. ДСВ X имеет закон распределения

x	0	1	2	3
p	0,1	0,3		0,2

Найти закон распределения СВ Y = sin(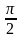 X) + 1.

2. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность, что при отсчете будет сделана ошибка, меньшая 0,04.

3. Найти минимальный объем выборки, при котором с надежностью 0,925 точность оценки матожидания нормально распределенной генеральной совокупности по выборочной средней равна 0,2, если среднее квадратичное отклонение генеральной совокупности равно 1,5.

4. Средний диаметр подшипников должен составлять 35 мм. Однако для выборки из 82 подшипников он составил 35,3 мм при «исправленном» среднем квадратичном отклонении 0,1 мм. При 5 %-м уровне значимости проверить утверждение о том, что станок, на котором изготавливают подшипники не требует подналадки.

Вариант 21

1. Плотность вероятности СВ X

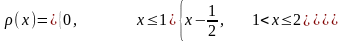
Найти функцию распределения и построить ее график.

2. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратичным отклонением 20 г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превышающей по абсолютной величине 10 г.

3. При обследовании средней зарплаты работающих жителей города была сделана выборка из 100 человек, при этом оказалось, что средняя выборочная равна 80 у.е., а несмещенная выборочная дисперсия равна 12. Найти доверительный интервал уровня 0,95 для средней зарплаты X.

4. Известно, что P(X<1)=0.98. В каких пределах находится M(X), если X-неотрицательная случайная величина?

Вариант 22

1. Следующая таблица представляет совместный закон распределения двух СВ X и Y – отдачи ( в % ) за первый год от инвестиций в отрасли А и В соответственно

X Y	-10	0	10	15
0	0,00	0,15	0,1	0,2
10	0,02	0,05	0,05	0,08
20	0,25	0,1	0,00	0,00

Рассчитать ожидаемые процентные отдачи от вложений только в одну из отраслей.

2. По техническим условиям средняя прочность троса составляет 2000 кг. В результате испытаний 20 кусков троса было установлено, что средняя прочность на разрыв равна 1955 кг при средней ошибке 25 кг. Удовлетворяет ли образец троса техническим условиям?

3. Анализируется доход населения, для чего извлечена выборка объема 300. По уровню дохода население подразделяется на 6 групп. Полученные по выборке данные сгруппированы в ИВР:

[ ,x )	[0,20)	[20,40)	[40,60)	[60,80)	[80,100)	[100,120)
n	10	50	80	100	40	20

Построить гистограмму частостей и выдвинуть предположение о виде закона распределения СВ X – дохода населения.

4. В каких пределах находится случайная положительная величина X с вероятностью 0,8, если M(X)=2 ?