
- •Вариант 0
- •Вариант 00
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 14
- •Вариант 15
- •2.Число вызовов «скорой помощи» за время t образует пуассоновский поток событий с параметром 2t. Чему равно среднее число вызовов за время ?
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
Вариант 0
1. Проведен маркетинговый анализ количества автомобилей в домохозяйствах района для определения целесообразности строительства станции техобслуживания. Обследовано 5000 домохозяйств. Из них в 250 автомобили отсутствовали, в 1500 было по 1 автомобилю, в 2500 – по 2, в 600 – по 3 и в 150 по 4. Вероятность поломки автомобиля в течение месяца равна 0,05. Станция будет рентабельна, если ее ежедневная загрузка составит 5 автомобилей. Целесообразно ли строительство станции в данном районе ?
2. При расфасовке некоторой продукции пакет считается стандартным, если его масса отличается от заданной массы 1 кг не более чем 20 г (в ту или иную сторону). Проверено, что при аккуратной работе ошибки массы подчиняются нормальному закону с матожиданием, равным 0, и средним квадратичным отклонением 10 г. Некоторая партия этой продукции из 10000 пакетов содержит 9000 стандартных пакетов. Соответствует ли это данному нормальному закону ?
3. Анализируется доход X фирм в отрасли, имеющий нормальное распределение. Предполагается, что средний доход в данной отрасли составляет не менее 1 млн $. По выборке из 49 фирм получены следующие данные: выборочная средняя равна 0,9 млн $ и S = 1,15 $. Не противоречат ли эти результаты выдвинутой гипотезе при уровне значимости 0,01 ?
4. Как определяются независимые случайные величины?
Вариант 00
1. В урне 8 шаров, из которых 5 белых, остальные – черные. Из нее вынимают наудачу 2 шара. Найти закон распределения числа белых шаров в выборке.
2. Число
вызовов «скорой помощи» за время t
образует пуассоновский поток событий
с параметром 2t. Чему равно
среднее число вызовов за время
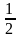 ?
?
3. Значения веса пойманной рыбы подчиняются нормальному распределению со средним 375 г, и
среднем квадратичном отклонением 25 г. Найти вероятность того, что вес одной рыбы будет больше 300 г.
4. Произведено
5 независимых наблюдений над СВ X
~ N (a,
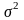 = 25). Результаты наблюдений таковы:
= 25). Результаты наблюдений таковы:
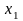 = - 25,
= - 25,
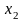 = 34,
= 34,
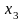 = - 20,
= - 20,
 = 10,
= 10,
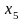 = 21. Найти оценку для a =
M(X), а также
построить для него 95 % доверительный
интервал.
= 21. Найти оценку для a =
M(X), а также
построить для него 95 % доверительный
интервал.
Вариант 1
1. Д.С.В. принимает значения 1, 3, 5 с вероятностями 0,2; 0,3; 0,5. Найти функцию распределения, математическое ожидание ДСВ.
2. Из 1500 деталей отобрано 100, распределение которых по размеру задано в таблице.
Размер детали |
8 – 8,2 |
8,2 – 8,4 |
8,4-8,6 |
8,6-8,8 |
8,8-9,0 |
Количество |
20 |
25 |
32 |
18 |
5 |
Найти реализацию оценки матожидания и несмещенной оценки дисперсии.
3. В данном регионе кандидата в парламент поддерживает 60 % населения. При опросе общественного мнения было выбрано 1000 человек. С какой вероятностью можно утверждать, что доля избирателей из этой выборки, поддерживающих кандидата, отличается от истинной доли не более чем на 0,02?
4. Производится экспериментальное определение среднего значения на разрыв образцов из двух различных сплавов. При измерении были получены следующие данные:
Сплав 1 |
4,52 |
3,63 |
3,99 |
5,00 |
6,39 |
3,22 |
4,9 |
|
|
|
Сплав2 |
4,66 |
7,04 |
6,27 |
4,19 |
4,81 |
6,65 |
5,56 |
4,6 |
6,19 |
6,16 |
Проверить гипотезу о равенстве средних, взяв α=0,01.
