Фазочастотная характеристика

Для нахождения аналитических выражений для ФЧХ коэффициента передачи цепи по напряжению нам нужно взять аргумент коэффициента передачи, это есть арктангенс отношения мнимой части к действительной.

Построим график фазо-частотных характеристик цепи для двух значений коэффициента усиления операторного усилителя =10 и =100 (Рисунок 1.3).

Рисунок 1.3 ФЧХ цепи для μ=10 (сплошная линия) и μ=100 (пунктир)

2. Анализ временных характеристик цепи Переходная характеристика цепи

где h(t) - переходная характеристика, p-оператор Лапласа.

Из формул (1.7) и (1.11) получим выражение для определения переходной характеристики:

Воспользуемся формулой (1.12) и данными таблицы1.1 и построим графики переходной характеристики для двух значений коэффициентов усиления операционного усилителя (Рисунок 1.4)

Рисунок 1.4 Переходная характеристика h(t) для μ=10 (сплошная линия) и μ=100 (пунктир)

Импульсная характеристика цепи

где g(t) - импульсная характеристика, p-оператор Лапласа.

Из формул (1.7) и (1.13) получим выражение для определения переходной характеристики:

Воспользуемся формулой (1.14) и данными таблицы1.1 и построим графики переходной характеристики для двух значений коэффициентов усиления операционного усилителя (Рисунок 1.5)

Рисунок 1.5 Импульсная характеристика g(t) для μ=10 (сплошная линия) и μ=100 (пунктир)

3. Прохождение импульсного сигнала через линейную цепь Нахождение выходного сигнала методом интеграла наложения

Найдем реакцию цепи на импульс, изображенный на рисунке:

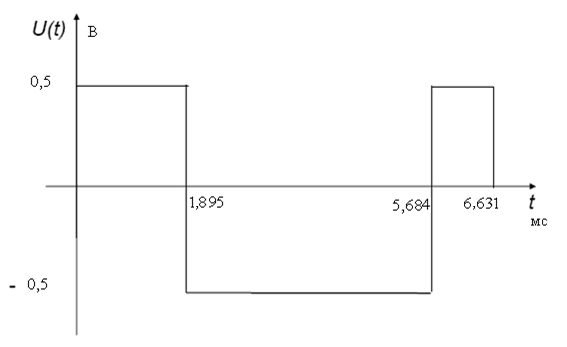
Рисунок 2.1 Входной импульсный сигнал

С помощью интеграла Дюамеля можно определить реакцию цепи на заданное воздействие и в том случае, когда внешнее воздействие на цепь описывается кусочно-непрерывной функцией, которая имеет конечное число конечных разрывов. В этом случае интервал интегрирования необходимо разбить на несколько промежутков в соответствии с интервалами непрерывности функции и учесть реакцию цепи на конечные скачки функции в точках разрыва. Для определения реакции цепи на воздействие импульса, см. рисунок 2.1, очевидно, что интервал интегрирования необходимо разбить на четыре части (t(0,t₁), t(t₁,t₂), t(t₂,t₃), t>t₃).

Воздействие на цепь имеет вид:

где

Для расчета реакции цепи удобно использовать следующую форму записи интеграла Дюамеля:

Поскольку на входе цепи действует сигнал, образованный совокупностью импульсов прямоугольной формы, см. рисунок2, для его аналитического представления используем функцию Хевисайда:

где 1(t) – функция Хевисайда.

Найдем выходной сигнал методом интеграла наложения с использованием переходной характеристики. При заданной форме входного сигнала на выходе имеем следующее:

В соответствии с формулой (2.4) и рисунком 2, построим импульс на выходе цепи для двух значений коэффициента усиления операционного усилителя (Рисунок 2.2).

Рисунок 2.2 Входной и выходные сигналы при различных значениях коэффициета усиления,

где u₂₁(t)- выходной сигнал при μ₁=10, u₂₂(t) – выходной сигнал при μ₂=100, u₁(t) – входной сигнал.

Увеличим длительность входного импульсного сигнала в 10 раз:

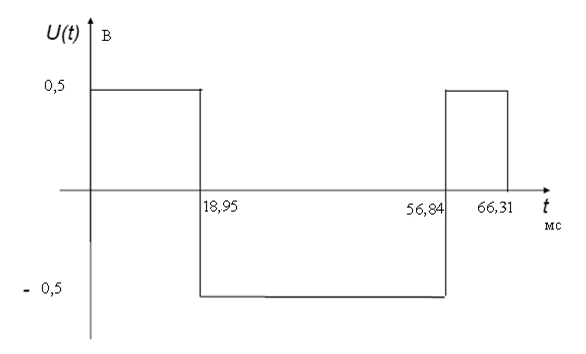
Рисунок 2.3 Входной импульсный сигнал

Графики входного и выходного сигналов:

Рисунок 2.4 Входной (сплошная линия) и выходной (пунктирная) сигнал при при длительности входного импульса, увеличенного в 10 раз