Так как наш «усилитель» инвертирующий, все импульсные и переходные характеристики «перевёрнуты» относительно оси 0х.

1.2.3 Определение постоянных времени цепи

Исходя из формулы (6), постоянные времени цепи будут определяться как величины, обратные модулю полюса передаточной функции:

(14)

Таблица 2. Значения τ в зависимости от μ

мю	τ, с
10	8.889*10^-5
100	8.889*10^-4

2.Прохождение импульсного сигнала через линейную цепь

С помощью интеграла Дюамеля можно определить реакцию цепи на заданное воздействие и в том случае, когда внешнее воздействие на цепь описывается кусочно-непрерывной функцией, которая имеет конечное число конечных разрывов. В этом случае интервал интегрирования необходимо разбить на несколько промежутков в соответствии с интервалами непрерывности функции и учесть реакцию цепи на конечные скачки функции в точках разрыва. Для определения реакции цепи на воздействие импульса изображённого на рис.2 очевидно, что интервал интегрирования необходимо разбить на четыре части ( t(0,t₁), t(t₁,t₂), t(t₂,t₃), t>t₃).

Параметры входного сигнала:

U_max = (m + n)/ 4 = 5/4 = 1,25 (В)

t1 = 8.889*10^-4 (c)

t2 = 2.667*10^-3 (c)

t3 = 3.111*10^-3 (c)

Для расчета реакции цепи на импульс запишу следующую форму интеграла Дюамеля:

, (15)

По виду импульса видно, что , поэтому в соответствии с условленным разбиением интервала, могу записать следующие выражения для выходного сигнала:

, (16)

При подстановке в приведенные выше выражения значений переходной характеристики для различных коэффициентов усиления получу окончательные выражения зависимости реакции от времени и построил график сначала для коэф. усиления 10, а потом для 100:

При μ=10 получаю что:

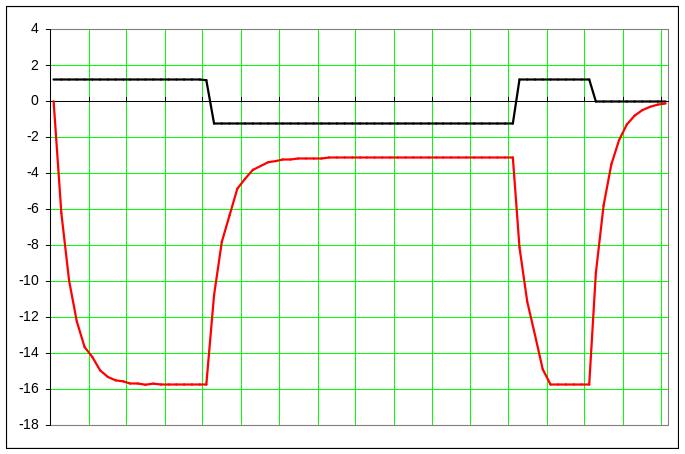
Рис 13. Графики входного и выходного сигналов при μ=10

При μ=100 имею:

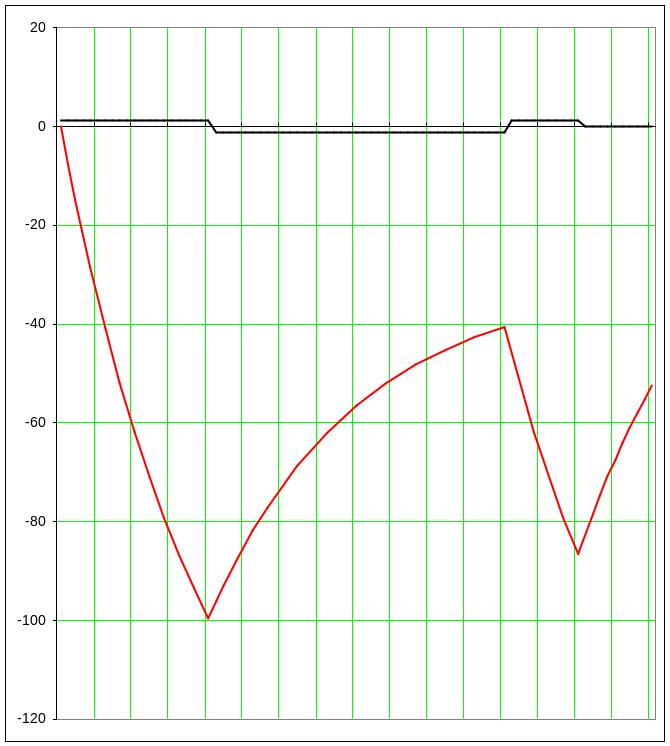
Рис 14.Графики входного и выходного сигналов при μ=100

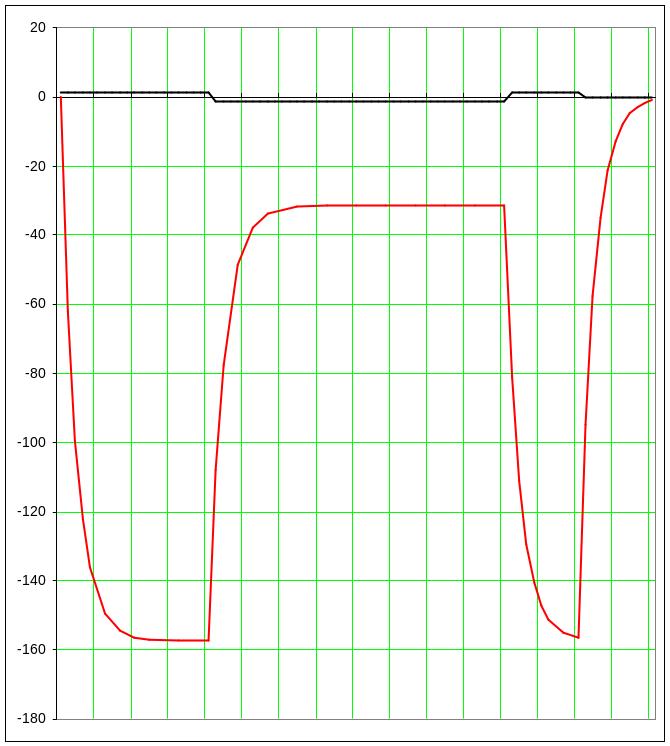
Рис 15. .Графики входного и выходного сигналов при μ=100 и длительности сигнала увеличенной в 10 раз

Заключение

В ходе выполнения данной работы был произведен анализ цепи, имеющей операционный усилитель. Была найдена операторная характеристика коэффициента передачи по напряжению этого усилителя, соответствующая ей комплексная частотная характеристика, найдены и построены графики амплитудно-частотной и фазочастотной характеристик для двух различных коэффициентов усиления. Далее были найдены и построены временные характеристики данной цепи: импульсная и переходная. И, наконец, используя переходную характеристику и интеграл наложения, были найдены реакции на импульсы при μ=10, μ=100, а так же при μ=100 и длительности импульса увеличенной в 10 раз.

Все полученные результаты в виде формул и графиков хорошо согласуются с теорией. В общем случае цепь является пропорционально – интегрирующей, что особенно явно видно при μ=10.