2.2. Перестановка данных и двоичная инверсия

Еще одной особенностью алгоритма с прореживанием по времени (как, впрочем, и большинства других алгоритмов БПФ) является необходимость такой перестановки элементов входной последовательности, чтобы выходная последовательность X(k) имела естественный (прямой) порядок расположения, т.е. k=0,1, ..., N-1. В примере на рис. 2.4 для этого требовался следующий порядок размещения входной последовательности: x(0), x(4), x(2), x(6), x(1), x(5), X(3), x(7). Характер перестановки элементов входной последовательности может быть описан сравнительно просто. В случае, когда N является степенью 2, входная последовательность должна быть расположена в памяти в двоично-инверсном порядке для того, чтобы выходная последовательность получилась в прямом порядке. Двоично-инверсный порядок определяется следующим образом. Если записать порядковые номера элементов входной последовательности в двоичном коде, используя L двоичных разрядов, причем N=2^L, а затем инвертировать порядок следования разрядов, то получаемые при этом числа и будут номерами элементов входной последовательности после их перестановки. Так, для случая N=8=2³ прямой порядок номеров приведен в таблице 2.1 слева, а двоично-инверсный - справа. Таким образом, для двоичной инверсии входной последовательности необходим соответствующий алгоритм.

Перестановку входной последовательности можно произвести с замещением, меняя в парах местами числа с прямыми и двоично-инверсными номерами и используя для этого лишь одну вспомогательную ячейку памяти.

Таблица 2 .1

Номер	Двоичное представление	Двоичная инверсия	Двоично-инверсный номер
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

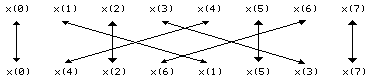Перестановку входной последовательности можно произвести с замещением, меняя в парах местами числа с прямыми и двоично-инверсными номерами и используя для этого лишь одну вспомогательную ячейку памяти.

Рис. 2.6

На рис. 2.6 показана схема перестановки данных, представленных в табл. 2.1.

Отметим еще одну особенность алгоритма БПФ, заключающуюся в том, что на всех этапах преобразования используются коэффициенты W^k_N, k=0, 1, ..., N-1. Существует несколько способов получения этих коэффициентов. Простейший способ - составление таблицы, к которой можно обращаться в процессе счета. Единственный недостаток этого способа заключается в том, что для хранения этих коэффициентов необходима дополнительная память примерно из N ячеек.

Второй способ заключается в непосредственном вычислении коэффициентов W^k_N=cos[(2/N)k]-jsin[(2/N)k] с использованием каждый раз стандартных подпрограмм расчета синуса и косинуса. Этот способ связан с большими затратами времени, поскольку вычисление этих функций, как правило, достаточно продолжительно.

Третий способ основан на применении простой рекуррентной формулы

с начальным условием W⁰_N=1, т. к. степени W на каждом этапе БПФ меняются с постоянным шагом. Так, в примере на рис. 2.4 на первом этапе используются коэффициенты W⁰ и W⁴, на втором - W⁰, W², W⁴, W⁶, а на третьем - W^k, k=0, 1, 2, ... , 7. Поэтому, чтобы иметь возможность на каждом из этапов использовать формулу (2.14), достаточно запомнить или вычислить только множители W⁴, W² и W⁰.