1.4. Взаимная связь спектров континуальных и дискретных сигналов

Допустим, что имеется непрерывный сигнал S(t) (рис. 1.7) в виде последовательности равноотстоящих импульсов, и этот сигнал задан на интервале [0,T), на котором умещается ровно N импульсов, например, N=4. Эти импульсы можно пронумеровать. Приняв номер импульса за новую дискретную переменную n, мы можем утверждать, что тот же рис. 1.7 изображает дискретный сигнал S(n), определенный на интервале [0,N). Оба эти сигнала, непрерывный S(t) и дискретный S(n), будут иметь дискретные спектры C_н(k) и C_д(k) (рис. 1.8). Эти спектры будут отличаться друг от друга.

Установим разницу между ними. Дискретная переменная на интервале [0,N) принимает только фиксированные значения n=0, 1, 2, ... , а непрерывная переменная t на интервале [0,T) принимает всевозможные значения. Таким образом, функция S(n) задает сигнал только в четырех точках, а функция S(t) - на бесконечном множестве точек, как совпадающих с точками отсчетов, так и в паузах между ними.

Рис. 1.7

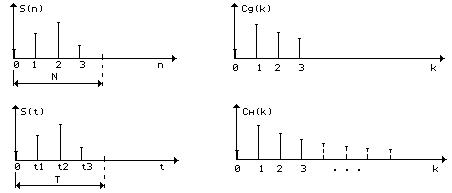
Рис. 1.8

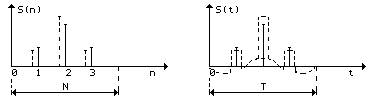
Рис. 1.9

Из этого различия вытекает важная особенность: разложение сигнала S(n) можно проводить только по системе дискретных решетчатых функций {(k,n)}, а разложение сигнала S(t) - только по системе непрерывных функций {(k,t)}. Спектры C_д(k) и С_н(k), полученные при таких разложениях (рис. 1.8), будут отличаться друг от друга тем, что спектр C_д(k) будет содержать только 4 (по числу степеней свободы дискретного сигнала), а спектр С_н(k) - бесконечное множество компонент, т. к. непрерывный сигнал S(t) имеет бесконечную размерность. Однако, поскольку сигнал S(t) задан на конечном интервале [0,T), его спектр будет дискретным. В отличие от спектра C_д(k), коэффициенты разложения С_н(k) будут бесконечно малыми, так как сигнал S(t) имеет бесконечно малую среднюю мощность (вследствие этого изображение спектра С_н(k) на рис. 1.8 является условным).

Чтобы продемонстрировать различие спектров C_д(k) и С_н(k), проведем следующий мысленный эксперимент. Опустим из этих спектров составляющую с одним и тем же номером. Это вызовет искажения сигнала (рис. 1.9), но в случае дискретного сигнала эти искажения будут выражаться только в изменении величин отсчетов (пунктирные линии), а в случае непрерывного сигнала помимо таких изменений в паузах между отсчетами еще появляются колебания.

Несмотря на указанное различие, спектры C_д(k) и С_н(k) принадлежат родственным сигналам и имеют некоторую общность, а именно: первые N коэффициентов разложения в этих спектрах совпадают с точностью до постоянного множителя.

Покажем, что это действительно так. Непрерывный сигнал S(t) может быть записан в виде

Перейдем к нормированному непрерывному времени =t/t и нормированному дискретному времен и n=[t/t], где t - интервал дискретизации, а [b] обозначает целую часть числа b, и введем дельта-функцию:

Спектр непрерывного сигнала S(t) будет определяться выражением

Подставим сюда выражение (1.5) для сигнала S(t ) в виде ряда Фурье:

Учитывая фильтрующее свойство дельта-функции, получим

Ранее было показано, что разложение дискретного сигнала имеет вид:

Сравнив (1.6) и (1.7), замечаем, что при k[0,N-1] спектры С_н(k) и C_д(k) совпадают с точностью до масштабного коэффициента. Из этого результата следует также, что у всех непрерывных огибающих данного дискретного сигнала с N отсчетами первые N/2 составляющих спектра совпадают с точностью до постоянного множителя. Таким образом, спектр дискретного сигнала одновременно определяет ансамбль непрерывных сигналов, порождающих данный дискретный сигнал. Чтобы выбрать из этого ансамбля конкретный непрерывный сигнал, необходимо знать дополнительно составляющие спектра при kN, которые отличают спектр непрерывной огибающей от спектра самого дискретного сигнала.

При разложении дискретного сигнала в ряд Фурье по системе комплексных экспоненциальных функций {e^jkn2/N} спектр является периодическим с периодом N. Другими словами, периодический дискретный сигнал S(n) и его спектр C(k) обладают свойством

где N - период, а b - произвольное целое число.

Действительно, спектр периодического дискретного сигнала при разложении по системе функций {e^jkn2/N} может быть записан в виде

Отсюда имеем

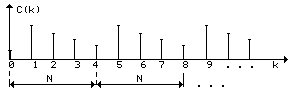
Рис. 1.10

При переходе от дискретного сигнала к непрерывному число отсчетов в одном периоде N, поэтому по мере приближения дискретного сигнала к непрерывному период его спектра будет неограниченно возрастать. В пределе, при N получим известную картину: периодический непрерывный сигнал имеет линейчатый, но непериодический спектр.