1.2. Проблемы в области спектрального оценивания

Интерес к цифровым методам спектрального анализа поддержива­ется тем улучшением характеристик, которое они обещают, а именно: высоким частотным разрешением, повышенной способностью к об­наружению слабых сигналов или же сохранением "досто­вер­нос­ти" формы спектра при меньшем числе используемых па­раметров. Аналитически описать характеристики большинства методов в случае ограниченного временного анализа (т. е. в случае корот­кой реа­ли­зации данных) весьма затруднительно, именно поэтому в ли­те­ратуре можно найти лишь очень малое количество эмпирических ре­зультатов. Это обусловило появление ряда проблем в области со­временного спектрального оценивания, некоторые из них кратко ос­вещены ниже.

1.2.1. Разрешение

Спектральное разрешение относится к числу главных проблем современного спектрального оценивания, в особенности примени­тельно к анализу коротких последовательностей данных. При этом то, что понимается под термином "разрешение", носит весьма субъек­тивный характер. Одно из ранних определений принадлежит Релею, которое исходит из следующего рабочего определения для разрешения оптических телескопов с ограниченной пространственной апертурой: "Подобно тому, как оптическая сила телескопа измеряется близостью двойных звезд, которые он может разрешить, так и оптическую силу спектроскопа следует измерять близостью самых близких двойных ли­ний в спектре, которые он может разрешить".

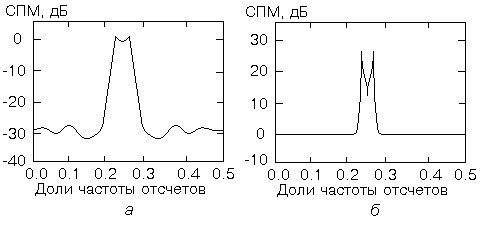
Рис. 1.2

В литературе принято характеризовать относительные величины разрешающей способности двух спектральных оценок на основе визу­альных наблюдений. Рассмотрим две спектральные оценки, показанные на рис. 1.2. Спектральная оценка на рис. 1.2, а имеет единичный нормиро­ванный максимум с двумя слабо различимыми пиками, что должно ука­зывать на присутствие двух спектральных составляющих. Если теперь нелинейным масштабированием сформировать новую спектральную функцию, которая показана на рис. 1.2, б, то она будет выглядеть, как спектр с "более высоким" раз­решением. На самом же деле оба приведенных спектра несут в себе одну и ту же информацию, а это означает, что одного лишь визуаль­ного сравнения спектральных оценок, конечно же, недостаточно для суждения о характеристиках разрешения.

1.2.2. Обнаружимость сигналов

Использование спектрального оценивания для обнаружения при­сутствия сигналов приводит к возникновению другой проблемы. Рас­смотрим периодограммы, показанные на рис. 1.3. Обе они соответствуют одной и той же 1024-точечной реализации некоторого процесса, со­стоящего из аддитивной смеси одной синусоиды и белого шума при отношении сигнал/шум равном -17 дБ. Периодограмма на рис. 1.3, а по­лу­чена непосредственно по всем 1024 отсчетам, и в ней над СПМ шума отчетливо видна спектральная линия синусоиды с относительной частотой 0.18 . На рис. 1.3, б представлена сглаженная периодограмма, полученная в результате разбиения исходной последовательности на 32 сегмента по 32 отсчета в каждом и последующего усреднения пе­риодограмм этих сегментов. На этой оценке более очевидна равномер­ная спектральная характеристика белого шума, но отклик, обуслов­ленный присутствием синусоиды, здесь не обнаружим. Можно пока­зать, что обнаружимость сигнала по несглаженной периодограмме превышает обнаружимость этого сигнала по сглаженной периодограмме в число раз, равное примерно корню квадратному из числа сегмен­тов, или на 10lg(32^1/2)=7.5 дБ в рассматриваемом случае. С точки зре­ния отображения полного спектра процесса (и оценки его СПМ) лучше сглаженная спектральная оценка, показанная на рис. 1.3, б, но с точки зрения обнаружимости сигнала - лучше

Рис. 1.3

несглаженная оценка.

Таким образом, аргументы в пользу выбора той или иной спек­тральной оценки будут зависеть от того, интересует ли нас сгла­женная оценка в пределах всего диапазона анализируемых частот или же нам важна более высокая степень обнаружимости сигнала на неко­торых конкретных его участках. Поэтому алгоритмы спектрального оценивания вовсе не обязательно являются также и хорошими алго­ритмами обнаружения.

1.2.3. О разграничении понятий оценивания параметров сигнала со

спектральным оцениванием

Задача спектрального оценивания подразумевает оценивание не­которой функции частоты. О характеристиках спектральной оценки судят по тому, насколько хорошо она согласуется с известным спек­тром тест-сигнала в некоторой непрерывной области частот. Имеются приложения, где основной интерес представляет лишь локальное по­ведение спектральной оценки в некоторых заданных диапазонах ча­стот. Примером может служить оценивание частоты синусоиды в белом шуме, результаты которого представлены на рис. 1.3. Нетрудно видеть, что в качестве спектральной оценки лучше использовать оценку на рис. 1.3, б, так как она ближе к равномерному спектру белого шума. В качестве же оценки частоты синусоиды лучше использовать оценку на рис. 1.3, а, так как она позволяет более точно определить частоту этой синусоиды. К сожалению, эти оценки нередко путают в литера­туре, поскольку многие задачи оценивания параметров излагаются в контексте спектрального оценивания, даже если функция спектраль­ной оценки не является искомой количественной величиной.

Задача оценивания параметров и задача спектрального оценива­ния требуют различного статистического подхода, хотя обе они могут перекрываться в некоторых частных случаях. Поэтому о характе­ристиках спектральной оценки нельзя полностью судить по ее харак­теристикам как оценки параметров. Так, например, сравнение оце­нок, представленных на рис. 1.3, показывает, что сглаженная перио­дограмма является хорошей спектральной оценкой, но плохой оценкой параметра, которым в данном случае является частота синусоиды.