7.9.2. Метод наименьших квадратов Прони

На практике число отсчетов данных N обычно превышает то минимальное их количество, которое необходимо для подгонки модели из p экспонент, т. е. N>2p. В этом переопределенном случае последовательность отсчетов данных может быть аппроксимирована лишь приблизительно с ошибкой аппроксимации e(n)=x(n)-x(n).

Одновременное отыскание порядка p и параметров {h_k,z_k}, 1kp, минимизирующих сумму квадратов ошибки

представляет собой трудную нелинейную задачу. Используя на первом и втором этапах метода Прони линейные процедуры НК, получим обобщенный метод Прони. В переопределенном случае линейное разностное уравнение (7.52) имеет вид:

где p+1nN. Член e(n) характеризует ошибку аппроксимации на основе ЛП в отличие от ошибки экспоненциальной аппроксимации (n). Уравнение (7.58) идентично уравнению для ошибки ЛП вперед, и тепрь парамеры a(m) из уравнения (7.52) можно выбирать как параметры, которые минимизируют не сумму (7.57), а сумму квадратов ошибок ЛП

Получим ковариационный метод ЛП. Существенно ограничение порядка: pN/2.

Метод Прони не позволяет получить оценку шума отдельную от сигнала. Модель Прони, учитывающая присутствие аддитивного шума, будет иметь форму

Если в исходной процедуре Прони вместо x(n) использовать x(n)-(n), то линейное разностное уравнение, которое описывает процесс, состоящий из суммы экспонент и аддитивного белого шума, будет иметь вид

На первом этапе метода Прони используется уравнение линейного предсказания

и попытка "отбеливания" e(n). Сравнивая два последних уравнения, видим, что отбеленный процесс e(n) совершенно не соответствует небелому СС-процессу, представленному выражением

Р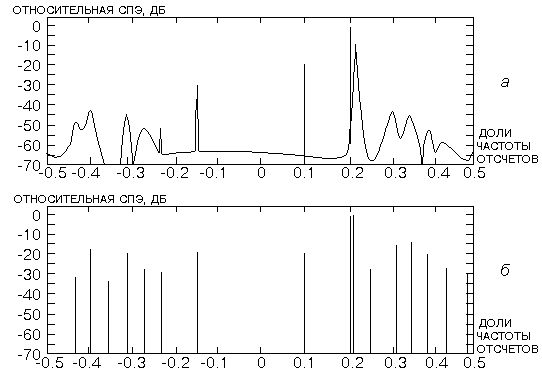 ис. 7.11. а - обобщенный метод Прони, р=15; б - модифицированный метод Прони, p=16.

Метод Прони не позволяет учесть наличие небелого шума в анализируемом процессе, поэтому при наличии сильного аддитивного шума получаются очень неточные, завышенные оценки коэффициентов затухания. Использование значений p, превышающих число действительно имеющихся полюсов, упрощает моделирование и позволяет учесть наличие шума.

Обычный МНК Прони может быть модифицирован для аппроксимации последовательности комплексных данных с помощью модели, состоящей из незатухающих комплексных синусоид - модифицированный метод Прони.

На рис. 7.11 показаны оценки по методу Прони СПЭ, полученные для 64-точечной тест-последовательности данных. Модифицированный метод Прони дает линейчатый спектр, т. к. в нем используется допущение о синусоидальной модели. Получаются очень точные оценки четырех действительных синусоид сигнала, но неточное представление окрашенного шума.

Условные обозначения, принятые в книге

▀ Скалярные переменные и скалярные функции обозначаются строчными латинскими и греческими буквами. Для обозначения преобразований от скалярных функций используются соответствующие прописные буквы.

▀ Векторы обозначаются строчными полужирными латинскими и греческими буквами.

▀ Матрицы обозначаются прописными полужирными латинскими и греческими буквами.

▀ Специальные обозначения:

Т – транспозиция вектора или матрицы;

Н – комплексно-сопряженная транспозиция вектора или матрицы;

* – комплексная сопряженность скаляра, вектора или матрицы;

^ – "крышка", используется для обозначения оценки.

Список аббревиатур

АКП – автокорреляционная последовательность;

АКФ – функция автокорреляции;

АПФК – критерий авторегрессионной передаточной функции;

АР – авторегрессионная модель (параметры);

АРСС – модель (параметры) авторегрессии – скользящего среднего;

БПФ – быстрое преобразование Фурье;

ВКП – взаимнокорреляционная последовательность;

ДВПФ – дискретно-временное преобразование Фурье;

ДПФ – дискретное преобразование Фурье;

ИКА – информационный критерий Акаике;

КИХ – конечная импульсная характеристика;

ЛП – линейное предсказание;

ЛЧМ – линейная частотная модуляция;

МНСК – метод наименьших средних квадратов;

ОБПФ – обратное быстрое преобразование Фурье;

ОДПФ – обратное дискретное преобразование Фурье;

ООП – окончательная ошибка предсказания;

ОПФ – обратное преобразование Фурье;

ПФ – преобразование Фурье;

РНК – рекурсивный алгоритм наименьших квадратов;

СПМ – спектральная плотность мощности;

СС – модель (параметры) скользящего среднего;

ФВК – функция взаимной корреляции;

ЦСА – цифровой спектральный анализ.

Список основных символов и сокращений

A_p – параметр авторегрессии p-го порядка;

– коэффициент ЛП назад р-го порядка ;

– коэффициент ЛП вперед р-го порядка ;

b – число разрядов цифрового числа;

B_e – эквивалентная ширина полосы в герцах;

B_s – эффективная статистическая ширина полосы в Гц;

b_q – параметр скользящего среднего q-го порядка;

C(k) – спектральные коэффициенты;

D{x} – дисперсия случайной переменной х;

D_N(f) – дискретная функция sinc, или ядро Дирихле;

Е – энергия сигнала;

e{x(n)} – математическое ожидание случайного процесса x(n);

– ошибка ЛП назад р-го порядка;

– ошибка ЛП вперед р-го порядка;

f – частота в Гц;

F – интервал дискретизации по частоте в Гц;

h(n) – импульсная характеристика фильтра;

H(z) – системная функция фильтра;

Im{x} – мнимая часть комплексной переменной х;

J – матрица отражения;

k – дискретная частота;

k_p=a_p(p) – коэффициент отражения порядка р;

L – размер ДПФ (число спектральных отсчетов) ;

n – дискретное время;

N – число отсчетов данных;

{(k,n)} – система дискретных базисных функций;

{(k,t)} – система непрерывных базисных функций;

p – порядок АР-модели или число периодограмм;

P_B(f) – оценка СПМ периодограммой Бартлетта;

P_D(f) – оценка СПМ периодограммой Даньелла;

P_W(f) – оценка СПМ периодограммой Уэлча;

P_xx(f) – спектральная плотность мощности;

P_xy(f) – взаимная спектральная плотность мощности;

P_xx(m) – дискретная СПМ;

q – порядок модели скользящего среднего;

Q – статистический критерий качества оценки;

rect(n) – прямоугольный импульс единичной высоты;

r_xx(m) – значение АКП при временном сдвиге m;

r_xy(m) – значение ВКП при временном сдвиге m;

Re{x} – вещественная часть комплексной переменной х;

SNR – линейное отношение сигнал/шум;

t – непрерывная временная переменная, секунды;

Т – интервал дискретизации по времени в секундах;

Т_е – эквивалентная временная протяженность в секундах;

w(n) – окно данных;

W(f) – преобразование Фурье окна данных;

W^k=W^p – коэффициенты БПФ (поворотные множители);

x(n) – функция дискретного времени;

x(t) – функция непрерывного времени;

u(n) – возбуждающий случайный процесс;

U – энергия дискретно-временного окна данных;

var{ } – дисперсия оценки параметра ;

z – комплексная переменная ;

(t) – дельта-функция Дирака;

(n) – единичная импульсная функция;

Ф(m) – автокорреляционная последовательность временного окна;

^b – среднеквадратичная ошибка (дисперсия ) ЛП назад;

^f – дисперсия ЛП вперед;

^fb – дисперсия ЛП вперед и назад;

– дисперсия белого шума;

(m) – корреляционное окно;

_e(m) – эффективное корреляционное окно;

(f) – ДВПФ корреляционного окна;

_e(f) – ДВПФ эффективного корреляционного окна;