5.2. Корреляционный анализ и спектральная оценка

Одной из важнейших временных характеристик сигнала является автокорреляционная функция (АКФ), позволяющая судить о степени связи сигнала с его сдвинутой по времени копией. Для действительной последовательности х(n) АКФ определяется в единицах мощности :

При m=0 значение АКФ достигает максимума и равно средней мощности сигнала х(n):

Для оценки степени подобия двух сигналов х(n) и y(n) используется функция взаимной корреляции (ФВК):

При m=0 значение ФВК определяет взаимную мощность сигналов х(n) и y(n) :

Функцию взаимной корреляции измеряют в случаях, когда последовательности х(n) и y(n) связаны операциями фильтрации и задержки. Например, в радиолокационных системах y(n) - это отфильтрованный, зашумленный и задержанный зондирующий сигнал х(n). В таких случаях положение максимума ФВК дает величину задержки входного сигнала, что является основой для решения многих задач радиолокации. Пусть, например, {х(n)}=(0,1,3,6,2,1,0,0) и y(n) сдвинута на два отсчета: {y(n)}=(3,6,2,1,0,0). Найдем ФВК: {z(m)}=(18/6, 36/6, 50/6, 32/6, 12/6, 3/6). Анализируя ФВК, находим ее максимум: z(2)=50/6. Номер (m=2) максимума соответствует сдвигу y(n) относительно х(n). На рис. 5.3 представлен пример двух сдвинутых на 28 отсчетов последовательностей и их функция взаимной корреляции.

Р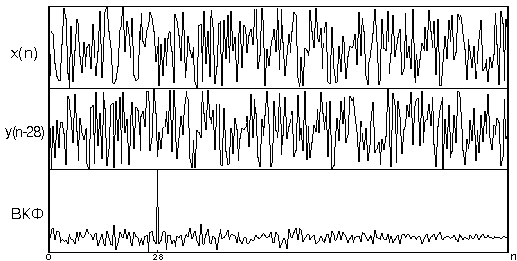 ис. 5.3

Спектральная плотность АКФ равна спектральной плотности мощности [6, с. 77]. Таким образом, спектральная плотность мощности (СПМ) определяется как ДВПФ автокорреляционной последовательности:

где r_xx(m) - функция автокорреляции, а N - число выборок x(n), 0nN-1.

Взаимная СПМ двух процессов х(n) и y(n) определяется как ДВПФ взаимной корреляционной последовательности:

где r_xy(m) - функция взаимной корреляции, а N - число выборок х(n) и y(n).

Функция СПМ описывает распределение мощности случайного процесса по частоте. В силу того, что функции АКФ и ВКФ имеют конечную длину, то бесконечные пределы суммирования заменяют на конечные. Если принять во внимание, что х(n) и y(n) имеют большое число выборок (N), то основная формула для вычислений АКФ и ФВК:

Предельные выражения показывают, что средние значения оценок сходятся при больших N к некоторому определенному постоянному числу. Формулы (5.17) и (5.18) хорошо работают при N>1024. Однако дисперсия оценки P_xx(f) и P_xy(f) будет сходится к нулю лишь при выполнении дальнейшего усреднения этих оценок.

Рассмотрим более подробно

1) метод получения оценки функции корреляции;

2) метод получения статистически устойчивых оценок СПМ на основе функции корреляции, получивший название корреляционного или коррелограмного метода оценки СПМ.

5.2.1. Метод получения оценки фвк

Рассмотрим последовательности х(n) и y(n). Их ДПФ:

Умножение X(k)Y(k) соответствует свертке х(n) и y(n) :

Таким образом, ФВК можно найти как ОДПФ от произведения ДПФ исходных последовательностей:

Причем х(n) и y(n) во всех выкладках считаются действительными.

Алгоритм получения оценки АКФ и ФВК опирается на метод быстрой свертки и для последовательностей х(n) и y(n) (0nN-1) выглядит следующим образом:

1) Вычислить x'(n)=x(n)w(n),

y'(n)=y(n)w(n).

2) Вычислить X(k)=БПФ{x'(n)},

Y(k)=БПФ{y'(n)}.

3) Вычислить оценку S_xy(k)=X(k)Y*(k).

4) Получить оценку ВКФ, выполнив r_xy(m)=ОБПФ{S_xy(k)}.

Схема алгоритма изображена на рис. 5.4.

Р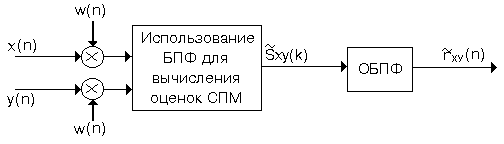 ис. 5.4

В этом методе алгоритм БПФ используется непосредственно для вычисления спектральной плотности мощности S_xy(k) на L дискретных частотах. Для уменьшения эффектов просачивания каждая из последовательностей умножается на сглаживающее окно w(n). После выполнения ОБПФ имеем искомую ФВК.