3.2. Соотношение между "скачущим" бпф и гребенкой фильтров
Выше было показано, что скользящее БПФ в точности эквивалентно анализу с использованием гребенки фильтров, поэтому возникает вопрос, какой из этих двух методов эффективнее с точки зрения объема вычислений. Не вдаваясь в детали, отметим, что при скользящем БПФ для каждого входного отсчета приходится вычислять полное БПФ, т. е. (N/2)log2N базовых операций на отсчет. При анализе с помощью гребенки фильтров, состоящей из гребенчатого фильтра, к выходу которого параллельно подключена группа цифровых резонаторов (рис. 3.3), число комплексных умножений на отсчет равно N. Таким образом, в большинстве случаев, представляющих интерес, гребенка фильтров оказывается эффективнее скользящего БПФ, поскольку в последнем случае не используются возможности итеративного расчета ДПФ. Однако ниже будет показано, что при определенных условиях алгоритм БПФ может оказаться эффективнее эквивалентной ему гребенки фильтров.
Р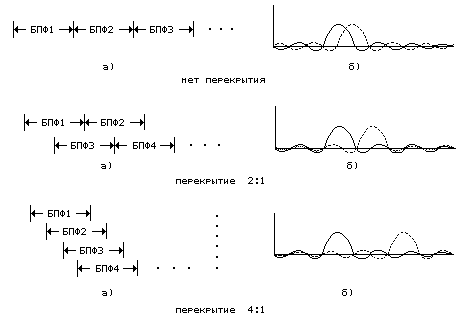
ис.
3.3
Для стандартного метода, позволяющего использовать БПФ для приближенного вычисления текущего спектра, характерно то, что интервал вычисления БПФ не скользит, а скачет. Несколько вариантов скачущего БПФ приведено на рис. 3.4, а, где представлены три из возможных способов размещения интервалов вычисления БПФ: с шагом, равным размеру БПФ, половине и четверти размера БПФ.
Вычислительная эффективность скачущего БПФ растет пропорционально величине "скачка", однако важно представить, как такой подход влияет на характер спектральных измерений. Отметим прежде всего, что скачущие измерения являются всего лишь отсчетами скользящих измерений. Следовательно, эквивалентный результат можно было бы получить, отбрасывая часть отсчетов на выходах гребенки фильтров.
Эффекты
такого прореживания можно проанализировать,
используя стандартную трактовку
наложения частот, вспомнив, что наложение
во временой области соответствует
дискретизации в частотной. На рис. 3.4, б
приближенно представлены эффекты
наложения частотных характеристик
эквивалентных фильтров для трех случаев
скачущего БПФ, приведенных на рис. 3.4,
а.
При отсутствии перекрытия
интервалов вычисления БПФ наблюдается
значительное наложение частотных
характеристик, что может привести к
серьезным искажениям спектральных
измерений. При перекрытии 2:1 и особенно
4:1 эффект наложения значительно
ослабляется, хотя и остается довольно
заметным. Таким образом, при увеличении
перекрытия интервалов анализа частотные
характеристики эквивалентных фильтров
анализатора оказываются более разнесенными
по частоте. На практике для
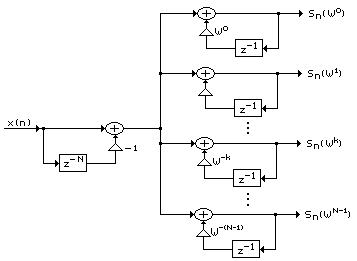Рис.
34
борьбы с наложениями используется метод взвешивания, который позволяет уменьшить уровень боковых лепестков и тем самым ослабить эффекты наложения. В качестве приближенной оценки этого эффекта можно использовать уровень наложенного спектра (он изображен пунктирной линией) в пределах главного лепестка фильтра.
4. Использование окон в спектральном анализе
Один из важных вопросов, который является общим для всех классических методов спектрального оценивания, связан с применением функции окна. Обработка с помощью окна (windowing) используется для управления эффектами, обусловленными наличием боковых лепестков в спектральных оценках. Заметим, что термин "взвешивание" (weighting) используется как синоним термина "обработка с помощью окна". Это контрастирует с практикой тех специалистов, которые употребляют термин "окно" только применительно к преобразованиям, связанным с применением весовой функции во временной области. Введение функции окна позволяет управлять формой частотных характеристик фильтров анализатора как в полосе пропускания, так и, что особенно важно, в полосе подавления. Функция W(f) является частотным окном в том случае, когда она получена в результате дискретно-временного преобразования Фурье (ДВПФ) окна данных w(n). Окна данных называются также обуживающими функциями (tapering functions), т. е. плавно спадающими к краям. Функция (f) обозначает спектральное окно в том случае, когда она является ДВПФ корреляционного окна (m), применяемого к дискретно-временной автокорреляционной последовательности. Основное назначение окна данных - уменьшить величину смещения в периодограммных спектральных оценках. Основное назначение корреляционного окна - уменьшить дисперсию коррелограммной оценки СПМ.