1.1 На указанной расчетной схеме в точке А изображена опора, которая называется:

1. шарнирно- подвижная

2. шарнирно-неподвижная

3. защемление

4. скользящая

5. упругая

1.2 На указанной расчетной схеме в точке В изображена опора, которая называется:

1. шарнирно- подвижная

2. шарнирно-неподвижная

3. защемление

4. скользящая

5. упругая

1.3 На указанной расчетной схеме в точке С изображена нагрузка, которая называется:

1. сосредоточенная сила

2. интенсивность

3. момент

4. пара сил

5. поперечная сила

1.4 На указанной расчетной схеме по длине элемента изображена нагрузка, которая называется:

1. сосредоточенная сила

2. интенсивность

3. момент

4. пара сил

5. поперечная сила

1.5 На указанной расчетной схеме величина момента в точке Д равна 10 т*м, сколько это будет в кн*м

1. 10

2. 98

3. 120

4. 1

5. 1000

1.6 На указанной расчетной схеме в точке А изображена опора, которая называется:

1. шарнирно- подвижная

2. шарнирно-неподвижная

3. защемление

4. скользящая

5. упругая

1.7 На указанной расчетной схеме в точке В изображена опора, которая называется

1. шарнирно- подвижная

2. шарнирно-неподвижная

3. защемление

4. скользящая

5. упругая

1.8 На указанной расчетной схеме в точке С изображена нагрузка, которая называется:

1. сосредоточенная сила

2. интенсивность

3. момент

4. пара сил

5. поперечная сила

1.9 На указанной расчетной схеме по длине элемента изображена нагрузка, которая называется

1. сосредоточенная сила

2. интенсивность

3. момент

4. пара сил

5. поперечная сила

1.10 На указанной расчетной схеме величина силы в точке Д равна 5 т, сколько это будет кн

1. 10

2. 49

3. 120

4. 75

5. 1000

1.11 На указанной расчетной схеме в точке А изображена опора, которая называется

1. шарнирно- подвижная

2. шарнирно-неподвижная

3. защемление

4. скользящая

5. упругая

1.12 На указанной расчетной схеме в точке В изображена опора, которая называется:

1. шарнирно- подвижная

2. шарнирно-неподвижная

3. защемление

4. скользящая

5. упругая

1.13 На указанной расчетной схеме в точке Д изображена нагрузка, которая называется:

1. сосредоточенная сила

2. интенсивность

3. изгибающий момент

4. пара сил

5. поперечная сила

1.14 На указанной расчетной схеме по длине элемента изображена нагрузка, которая называется:

1. сосредоточенная сила

2. интенсивность

3. момент

4. пара сил

5. поперечная сила

1.15 На указанной расчетной схеме величина момента в точке Д равна 3 т*м, сколько это будет кн*м.

1. 10

2. 29,4

3. 120

4. 75

5. 1000

2.1 На указанной расчетной схеме величина опорной реакции в точке В равна:

1. 48 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.2 На указанной расчетной схеме величина опорной реакции в точке А равна:

1. 15 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.3 На указанной расчетной схеме величина опорной реакции в точке В равна:

1. 35 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.4 На указанной расчетной схеме величина опорной реакции в точке А равна:

1. 150 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.5 На указанной расчетной схеме величина опорной реакции в точке В равна:

1. 150 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.6 На указанной расчетной схеме величина опорной реакции в точке А равна:

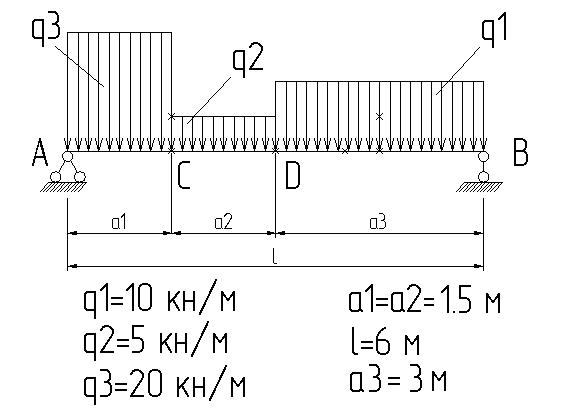
1. 23,44 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.7 На указанной расчетной схеме величина опорной реакции в точке В равна:

1. 38,43 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.8 На указанной расчетной схеме величина опорной реакции в точке А равна:

1. 73 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.9 На указанной расчетной схеме величина опорной реакции в точке В равна:

1. 47 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.10 На указанной расчетной схеме величина опорной реакции в точке А равна:

1. 1,62 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.11 На указанной расчетной схеме величина опорной реакции в точке В равна:

1. -2,64 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.12 На указанной расчетной схеме величина опорной реакции в точке А равна:

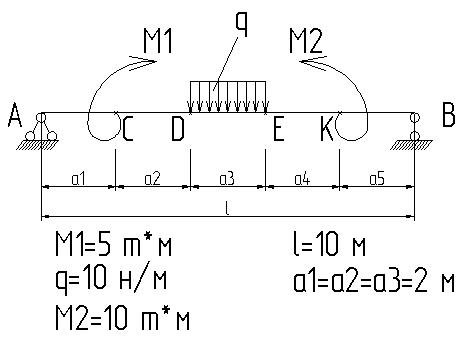
1. -2,64 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.13 На указанной расчетной схеме величина опорной реакции в точке В равна:

1. 4,99 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.14 На указанной расчетной схеме величина опорной реакции в точке А равна:

1. 70,79 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000 н

2.15 На указанной расчетной схеме величина опорной реакции в точке А равна:

1. 48 кн

2. 29,4 кн

3. 120 кн

4. 75 кн

5. 1000н

3.1 Какая дисциплина изучает равновесие и движение твердых тел?

1. Теоретическая механика

2. Сопротивление материалов

3. Теория упругости

4. Строительная механика

5. Физика

3.2 В какой дисциплине рассматриваются тела, которые могут менять размеры и форму под действием сил?

1. Теоретическая механика

2. Сопротивление материалов

3. Теория упругости

4. Строительная механика

5. Физика

3.3 Как называется совокупность наук о прочности, жесткости и устойчивости?

1. Теоретическая механика

2. Сопротивление материалов

3. Теория упругости

4. Строительная механика

5. Физика

3.4 Изменение взаимного расположения частиц, при котором изменяются размеры, объем и форма, а количество вещества остается постоянным называется:

1. Деформацией

2. Удлинением

3. Укорочением

4. Изгибом

5. Прогибом

3.5 Часть деформации, которая исчезает после снятия нагрузки, называется:

1. Упругой

2. Остаточной

3. Пластической

4. Априорной

5. Конструктивной

3.6 Часть деформации, которая остается после снятия нагрузки называется:

1. Упругой

2. Остаточной

3. Пластической

4. Априорной

5. Конструктивной

3.7 Если деформации после снятия нагрузки полностью исчезли, то тело называют:

1. Абсолютно упругим

2. Изотропным

3. Анизотропным

4. Априорным

5. Конструктивным

3.8 Если упругие свойства тела одинаковы во всех направлениях, то тело называют:

1. Абсолютно упругим

2. Изотропным

3. Анизотропным

4. Априорным

5. Конструктивным

3.9 Если упругие свойства тела во всех направлениях различны, то тело называют:

1. Абсолютно упругим

2. Изотропным

3. Анизотропным

4. Априорным

5. Конструктивным

3.10 Нагрузка от снега, давления ветра, гололеда называется:

1. Объемной

2. Поверхностной

3. Внешней

4. Внутренней

5. Переменной

3.11 Равномерное распространение нагрузки по длине элемента называется:

1. Интенсивностью

2. Распределенностью

3. Динамичностью

4. Равномерностью

5. Переменностью

3.12 Модель заместитель модели оригинала для возможности выполнения расчетов называется:

1. Расчетной схемой

2. Конструктивной схемой

3. Дискретной схемой

4. Априорной схемой

5. Эскизной схемой

3.13 Модель «заместитель объекта оригинала» называют:

1. Расчетной схемой

2. Конструктивной схемой

3. Дискретной схемой

4. Априорной схемой

5. Эскизной схемой

3.14 Опора, запрещающая деформацию тела, называется:

1. Шарнирно-подвижная

2. Шарнирно-неподвижная

3. Защемление

4. Условно-подвижная

5. Заделка

3.15 Опора, позволяющая деформацию тела в двух направлениях, называется:

1. Шарнирно-подвижная

2. Шарнирно-неподвижная

3. Защемление

4. Условно-подвижная

5. Заделка

4.1 Опора, позволяющая деформацию тела в одном направлении, называется:

1. Шарнирно-подвижная

2. Шарнирно-неподвижная

3. Защемление

4. Условно-подвижная

5. Заделка

4.2 Равнодействующая внутренних нормальных сил упругости в поперечном сечении бруса называется:

1. Продольной силой

2. Поперечной силой

3. Изгибающим моментом

4. Результирующей силой

5. Равнодействующей силой

4.3 Поперечное сечение бруса, плоское и нормальное к его оси до деформации, остается плоским и нормальным к его оси после деформации - это:

1. Гипотеза Бернулли

2. Закон распределения нормальных напряжений

3. Закон Гука

4. Закон Шеннона

5. Закон Ньютона

4.4 В поперечном сечении бруса при центральном растяжении и сжатии возникают равномерно- распределенные и нормальные напряжения, равные отношению продольной силы к площади поперечного сечения - это:

1. Гипотеза Бернулли

2. Закон распределения нормальных напряжений

3. Закон Гука

4. Закон Шеннона

5. Закон Ньютона

4.5 Абсолютное удлинение (укорочение) прямо пропорционально величине силы и длине бруса и обратно пропорционально модулю продольной упругости и площади поперечного сечения бруса:

1. Гипотеза Бернулли

2. Закон распределения нормальных напряжений

3. Закон Гука

4. Закон Шеннона

5. Закон Ньютона

4.6 Проекция равнодействующей внутренних сил упругости на ось У называется:

1. Продольной силой

2. Поперечной силой

3. Изгибающим моментом

4. Результирующей силой

5. Равнодействующей силой

4.7 Момент равнодействующей внутренних сил относительно центра тяжести рассматриваемого сечения называется:

1. Продольной силой

2. Поперечной силой

3. Изгибающим моментом

4. Результирующей силой

5. Равнодействующей силой

4.8 Изгибающий момент в поперечном сечении бруса, когда на левом торце правой части он направлен по часовой стрелке, а на правом торце левой части против часовой стрелки считается:

1. Положительным

2. Отрицательным

3. Переменным по знаку

4. Принимается по модулю

5. Равным нулю

4.9 Продольная сила в сечении при растяжении считается:

1. Положительным

2. Отрицательным

3. Переменным по знаку

4. Принимается по модулю

5. Равная нулю

4.10 Поперечная сила, когда на левом торце правой части она направлена, снизу вверх называется:

1. Положительной

2. Отрицательной

3. Переменной по знаку

4. Принимается по модулю

5. Равная нулю

4.11 Относительно некоторой оси взятая по площади F сумма произведений элементарных площадок на их расстояния до этой оси называется:

1. Статическим моментом

2. Экваториальным моментом

3. Полярным моментом

4. Центробежным моментом

5. Изгибающим момоентом

4.12 Относительно некоторой оси взятая по площади F сумма произведений элементарных площадок на квадраты их расстояний до этой оси называется:

1. Статическим моментом

2. Экваториальным моментом

3. Полярным моментом

4. Центробежным моментом

5. Изгибающим моментом

4.13 Относительно некоторой точки взятая по площади F сумма произведений элементарных площадок на квадраты их расстояний до этой точки называется:

1. Статическим моментом

2. Экваториальным моментом

3. Полярным моментом

4. Центробежным моментом

5. Изгибающим моментом

4.14 Относительно некоторых двух взаимно перпендикулярных осей по площади F сумма произведений элементарных площадок на расстояния до этих осей называется:

1. Статическим моментом

2. Экваториальным моментом

3. Полярным моментом

4. Центробежным моментом

5. Изгибающим моментом

4.15 Укажите граничные условия первой группы предельных состояний для изгибаемых элементов:

A) N< Ф

B)  _пр

C) М W

D) l l_пр

E) M<=R_вtW_pl

5.1 Укажите граничные условия второй группы предельных состояний для изгибаемых элементов:

A) N< Ф

B)  _пр

C) М W

D) l l_пр

E) M<=R_вtW_pl

5.2 Потеря несущей способности и непригодность к эксплуатации это:

1. Первая группа предельных состояний

2. Вторая группа предельных состояний

3. Третья группа предельных состояний

4. Четвертая группа предельных состояний

5. Пятая группа предельных состояний

5.3 Непригодность к нормальной эксплуатации это:

1. Первая группа предельных состояний

2. Вторая группа предельных состояний

3. Третья группа предельных состояний

4. Четвертая группа предельных состояний

5. Пятая группа предельных состояний

5.4 Наибольшее напряжение, до которого относительные деформации изменяются прямо пропорционально напряжениям, называется:

1. Пределом пропорциональности

2. Пределом упругости

3. Пределом текучести

4. Пределом прочности

5. Допускаемым напряжением

5.5 Наибольшее напряжение, при котором образец получает весьма малую остаточную деформацию, называют:

1. Пределом пропорциональности

2. Пределом упругости

3. Пределом текучести

4. Пределом прочности

5. Допускаемым напряжением

5.6 Наибольшее напряжение, при котором деформации образца растут без увеличения нагрузки, называют:

1. Пределом пропорциональности

2. Пределом упругости

3. Пределом текучести

4. Пределом прочности

5. Допускаемым напряжением

5.7 Напряжение вызываемое, наибольшей нагрузкой на образец за время опыта и отнесенное к первоначальному сечению бруса называют:

1. Пределом пропорциональности

2. Пределом упругости

3. Пределом текучести

4. Пределом прочности

5. Допускаемым напряжением

5.8 Каталоги, поставляемых металлургическими заводами листов, профилей с указанием их формы, размеров, геометрических характеристик, массы называют:

1. Перечнем

2. Сортаментом

3. Указателем

4. Каталогом

5. Реестром

5.9 Круг, квадрат, полоса, уголки - это:

1. Сортовая сталь

2. Фасонная сталь

3. Универсальная сталь

4. Гнутая сталь

5. Сварная сталь

5.10 Отношение абсолютной линейной деформации к первоначальной длине бруса называют:

1. относительной деформацией

2. жесткостью

3. напряжением

4. сжатием

5. модулем упругости

5.11 Двутавры, швеллеры, шпунтовые и другие профили – это:

1. Сортовая сталь

2. Фасонная сталь

3. Универсальная сталь

4. Гнутая сталь

5. Сварная сталь

5.12 Дискретная схема сооружения отображает:

1. Номер конечного элемента

2. Номер узла

3. Номер типа жесткости

4. Номер конечного элемента, номер узла, номер типа жесткости

5. Характер деформации сооружения

5.13 Расчетное значение нагрузки получают путем умножения:

1. Высоты сечения на плотность

2. Высоты сечения на объемный вес

3. Нормативного значения нагрузки на коэффициент надежности по нагрузки

4. Нормативного значения нагрузки на высоту сечения

5. Нормативного значения нагрузки на площадь поперечного сечения

5.14 На какие усилия рассчитывается продольная рабочая арматура в изгибаемом железобетонном элементе:

A) N – продольная сила

B) Q – поперечная сила

C)  - изгибающий момент

D) R₀ – кубиковая прочность

E) _s – нормальное напряжение

5.15 На какие из предложенных усилий рассчитываются поперечные стержни в изгибаемом железобетонном элементе:

A) N – продольная сила

B) Q – поперечная сила

C)  - изгибающий момент

D) R₀ – кубиковая прочность

E) _s – нормальное напряжение

6.1 В какой зоне сечения изгибаемого железобетонного элемента устанавливается рабочая арматура:

1. в зоне максимальной продольной силы – N

2. в зоне изгибаемых моментов - 

3. в зоне максимальной поперечной силы – Q

4. в сжатой зоне бетона

5. в зоне максимального линейного удлинения

6.2 По какому из предложенных условий выполняется проверка несущей способности изгибаемого бетона элемента:

1. M<=R_вtW_pl

2. M<=R_b*A_b*(h₀-x/2)

3. M<=R_b*A_b*(h₀-x/2)+R_sc*A_c’*(h₀-a’)

4. M<= R_b*A_b*(h₀+d-0.5x)

5. M<= 0.3*_w1*_b1*R_b*b*h0

6.3 По какому из предложенных условий выполняется проверка несущей способности плиты перекрытия на «комнату» в плоскости нормальной к продольной оси элемента:

1. M<=R_вtW_p

2. M<=R_b*A_b*(h₀-x/2)

3. M<=R_b*A_b*(h₀-x/2)+R_sc*A_c’*(h₀-a’)

4. M<= R_b*A_b*(h₀+d-0.5x)

5. M<= 0.3*_w1*_b1*R_b*b*h0

6.4 По какому из предложенных условий выполняется проверка несущей способности ригеля, либо пустотной плиты перекрытия жилого дома в плоскости нормальной к продольной оси элемента:

1. M<=R_вtW_p

2. M<=R_b*A_b*(h₀-x/2)

3. M<=R_b*A_b*(h₀-x/2)+R_sc*A_c’*(h₀-a’)

4. M<= Rb*Ab*(h0+d-0.5x)

5. M<= 0.3*_w1*_b1*R_b*b*h0

6.5 По какому условию выполняется проверка несущей способности сжатого бетонного элемента:

1. N<=(*R_bt*W_pl)/(e₀*-r)

2. M<=*R_bt*W_pl

3. Q<=0.3*_w1*_b1*R_b*b*h0

4. Q<=Q_b+Q_sw+Q_s,inc

5. M<=R_b*A_b*(h₀-x/2)+R_sc*A_c’*(h₀-a’)

6.6 Какое из условий прочности внецентренно- сжатых железобетонных элементов справедливо при условии <_R:

1. N+_s*A_s-R_sc*A_s’=R_b*b*x

2. N+R_s*A_s =R_b*b*x

3. N*e<=R_b*b*x*(h₀-0.5*x)+R_sc*A_s’*(h₀-a’)

4. Q<=Q_b+Q_sw+Q_s,inc

5. M<=R_b*A_b*(h₀-x/2)+R_sc*A_c’*(h₀-a’)

6.7 По какому условию выполняется проверка несущей способности центрально-растянутых бетонных элементов:

1. N<=_s6*R_s*A_sp+R_s*A_s

2. N<=(*R_bt*W_pl)/(e₀*-r)

3. N+_s*A_s-R_sc*A_s’=R_b*b*x

4. N+R_s*A_s =R_b*b*x

5. M<=R_b*A_b*(h₀-x/2)+R_sc*A_c’*(h₀-a’)

6.8 По какому условию выполняется проверка несущей способности растянутых элементов, когда внешняя сила расположена между равнодействующими силами, приложенными к рабочей арматуре:

1. N<=_s6*R_s*A_sp+R_s*A_s

2. N<=(*R_bt*W_pl)/(e₀*-r)

3. N+_s*A_s-R_sc*A_s’=R_b*b*x

4. N+R_s*A_s =R_b*b*x

5. M<=R_b*A_b*(h₀-x/2)+R_sc*A_c’*(h₀-a’)

6.9 По какому условию выполняется проверка несущей способности растянутых элементов, когда внешняя сила расположена за пределами расстояний между равнодействующими:

1. N*e<=_s6*R_s*A_sp’*(h₀-a_p’)+R_s*A_s’*(h₀-a_s’)

2. N+R_s*A_s-R_s*A_s’=R_b*b*x

3. N*e<=Rb*Abc*Zb+R_s*A_s’*(h₀-a_s’)+_sc*A_sp’*(h₀-a_p’)

4. N<=(*R_bt*W_pl)/(e₀*-r)

5. M<=R_b*A_b*(h₀-x/2)+R_sc*A_c’*(h₀-a’)

6.10 Требуемый момент сопротивления прокатных балок определяют по формуле:

1. 

2. N+R_s*A_s-R_s*A_s’=R_b*b*x

3. N*e<=Rb*Abc*Zb+R_s*A_s’*(h₀-a_s’)+_sc*A_sp’*(h₀-a_p’)

4. N<=(*R_bt*W_pl)/(e₀*-r)

5. M<=R_b*A_b*(h₀-x/2)+R_sc*A_c’*(h₀-a’)

6.11 Состояние конструкции при переходе за которое она перестает удовлетворять нормальным эксплуатационным требованиям называется:

1. Неопределенным

2. Неуравновешенным

3. Пластическим

4. Разрушающим

5. Предельным

6.12 Состояние обеспечивающее прочность, устойчивость, усталость материала относят к:

1. Первой группе предельных состояний

2. Второй группе предельных состояний

3. Третьей группе предельных состояний

4. Четвертой группе предельных состояний

5. Пятой группе предельных состояний

6.13 Состояние при котором конструкцию нельзя эксплуатировать называется:

1. Неопределенным

2. Неуравновешенным

3. Пластическим

4. Разрушающим

5. Предельным

6.14 Состояние обеспечивающее предельные деформации, образование и раскрытия трещин относят к:

1. Первой группе предельных состояний

2. Второй группе предельных состояний

3. Третьей группе предельных состояний

4. Четвертой группе предельных состояний

5. Пятой группе предельных состояний

6.15 Произведение нормативного сопротивления на коэффициент однородности материала называется:

1. Коэффициентом надежности по нагрузке

2. Коэффициентом условия работы

3. Расчетным сопротивлением материала

4. Расчетными нагрузками

5. Расчетной несущей способностью

7.1 Конструкции, служащие для укрепления берегов и имеющие в плане прямолинейное, ломанное и криволинейное очертание, называют:

1. Подпорными стенками.

2. Удерживающими конструкциями.

3. Укрепляющими стенками.

4. Крепежом.

5. Ограждением.

7.2 Подпорные стенки (пс), размерами поперечного сечения до 0,75 м называют:

1. Сборными пс.

2. Ряжевыми пс.

3. Массивными пс.

4. Монолитными пс.

5. Одевающими пс.

7.3 Конструкцию, укрепляющую грунт берега с целью оформления поверхности, называют:

1. Сборными подпорными стенками.

2. Ряжевыми подпорными стенками.

3. Массивными подпорными стенками

4. Монолитными подпорными стенками.

5. Одевающими подпорными стенками.

7.4 Конструкцию из железобетона уголкового типа заводского изготовления, служащую для укрепления грунта берега, называют:

1. Сборными подпорными стенками.

2. Ряжевыми подпорными стенками.

3. Массивными подпорными стенками.

4. Монолитными подпорными стенками.

5. Одевающими подпорными стенками.

7.5 Конструкцию из железобетона уголкового типа, изготавливаемую на месте, служащую для укрепления грунта берега, называют:

1. Сборными подпорными стенками.

2. Ряжевыми подпорными стенками.

3. Массивными подпорными стенками.

4. Монолитными подпорными стенками.

5. Одевающими подпорными стенками.

7.6 Конструкцию из железобетона с заполнением внутренней полости грунтом для укрепления грунта берега, называют:

1. Сборными подпорными стенками.

2. Ряжевыми подпорными стенками.

3. Массивными подпорными стенками.

4. Монолитными подпорными стенками.

5. Одевающими подпорными стенками.

7.7 Увязку инженерных сооружений с генеральным планом, архитектурным ансамблем застройки относят к:

1. Архитектурно- планировочным требованиям.

2. Производственно - эксплуатационным требованиям.

3. Расчетно-конструктивным требованиям.

4. Экономическим требованиям.

5. Экологическим требованиям.

7.8 Назначение ширины ездового полотна, устройство водоотвода, удобство механизированных работ во время ремонтов относят к:

1. Архитектурно- планировочным требованиям.

2. Производственно - эксплуатационным требованиям.

3. Расчетно-конструктивным требованиям.

4. Экономическим требованиям.

5. Экологическим требованиям.

7.9 Соответствие сечений инженерных сооружений условиям прочности, устойчивости, жесткости относят к:

1. Архитектурно- планировочным требованиям.

2. Производственно - эксплуатационным требованиям.

3. Расчетно-конструктивным требованиям.

4. Экономическим требованиям.

5. Экологическим требованиям

7.10 Назначение затрат на возведение инженерных сооружений с учетом вариантной проработки относят к:

1. Архитектурно- планировочным требованиям.

2. Производственно - эксплуатационным требованиям.

3. Расчетно-конструктивным требованиям.

4. Экономическим требованиям.

5. Экологическим требованиям.

7.11 Проектное очертание в плане береговой линии, соответствующей меженнему уровню воды называют:

1. Линией регулирования.

2. Береговой линией

3. Красной линией

4. Предохранительной линией

5. Планировочной линией

7.12 Линия регулирования определяет:

1. Уровень воды в реке

2. Русло реки

3. Проектную ширину рек

4. Ширину проездов вдоль реки

5. Линию зеленых насаждений

7.13 Чему равно расстояние между деформационными швами в бетонных и одевающих подпорных стенках?

1. 5-6 м

2. 6-8 м

3. 8-10 м

4. 10-15 м

5. 15-20 м

7.14 Чему равно расстояние между деформационными швами в железобетонных подпорных стенках?

1. 40 м

2. 6-8 м

3. 8-10 м

4. 10-15 м

5. 15-20 м

7.15 Толщина массивной подпорной стенки в месте сопряжения с фундаментом при высоте Н должна быть:

1. 0.2 Н

2. (0.35-0.40)Н

3. 0.5Н

4. 1,5Н

5. Н

8.1 Величину расчетного горизонтального давления грунта от засыпки с горизонтальной поверхностью и на единицу площади вертикальной стенки определяют по формуле:

1. p=n_Г H tg²(45- /2)

2. P_В=n_В q tg²(45- /2)

3. p₁=_o h₁ – n_Гh₁_o(1-n)tg²(45- /2)

4. p₂=_o h₂

5. p₃= n_Г [ - _o(1-n)] h₃ tg²(45- /2)

8.2 Величину равномерно распределенной нагрузки с интенсивностью q, в качестве горизонтального давления в любой точке по высоте определяют по формуле:

1. p=n_Г H tg²(45- /2)

2. P_В=n_В q tg²(45- /2)

3. p₁=_o h₁ – n_Гh₁_o(1-n)tg²(45- /2)

4. p₂=_o h₂

5. p₃= n_Г [ - _o(1-n)] h₃ tg²(45- /2)

8.3 Величину гидравлического давления грунтовой воды определяют по формуле:

1. p=n_Г H tg²(45- /2)

2. P_В=n_В q tg²(45- /2)

3. p₁=_o h₁ – n_Гh₁_o(1-n)tg²(45- /2)

4. p₂=_o h₂

5. p₃= n_Г [ - _o(1-n)] h₃ tg²(45- /2)

8.4 Величину давления со стороны реки определяют по формуле:

1. p=n_Г H tg²(45- /2)

2. P_В=n_В q tg²(45- /2)

3. p₁=_o h₁ – n_Гh₁_o(1-n)tg²(45- /2)

4. p₂=_o h₂

5. p₃= n_Г [ - _o(1-n)] h₃ tg²(45- /2)

8.5 Величину давления взвешенного грунта определяют по формуле:

1. p=n_Г H tg²(45- /2)

2. P_В=n_В q tg²(45- /2)

3. p₁=_o h₁ – n_Гh₁_o(1-n)tg²(45- /2)

4. p₂=_o h₂

5. p₃= n_Г [ - _o(1-n)] h₃ tg²(45- /2)

8.6 Равнодействующая от давления грунта со стороны засыпки на вертикальную плоскость подпорной стенки определяется по формуле:

1. Е=0,5рН

2. Е₁=0,5р₁h₁

3. Е_В=qH

4. Е₂= 0,5 р₂h₂

5. Е₃= 0,5 р₃h₃

8.7 Равнодействующая от давления распределенной нагрузки с интенсивностью q на вертикальную плоскость подпорной стенки определяется по формуле:

1. Е=0,5рН

2. Е₁=0,5р₁h₁

3. Е_В=qH

4. Е₂= 0,5 р₂h₂

5. Е₃= 0,5 р₃h₃

8.8 Равнодействующая от давления грунтовой воды определяют по формуле:

1. Е=0,5рН

2. Е₁=0,5р₁h₁

3. Е_В=qH

4. Е₂= 0,5 р₂h₂

5. Е₃= 0,5 р₃h₃

8.9 Равнодействующая от давления реки определяют по формуле:

1. Е=0,5рН

2. Е₁=0,5р₁h₁

3. Е_В=qH

4. Е₂= 0,5 р₂h₂

5. Е₃= 0,5 р₃h₃

8.10 Равнодействующая от давления взвешенного грунта определяют по формуле:

1. Е=0,5рН

2. Е₁=0,5р₁h₁

3. Е_В=qH

4. Е₂= 0,5 р₂h₂

5. Е₃= 0,5 р₃h₃

8.11 Момент, опрокидывающий стенку и равный сумме моментов всех горизонтальных и вертикальных сил относительно центра тяжести площади опирания фундамента, называется:

1. Предельный момент

2. Удерживающий момент

3. Изгибающий момент

4. Крутящий момент

5. Опрокидывающий момент

8.12 Момент, воспринимаемый стенкой и равный сумме всех вертикальных сил, умноженных на расстояние – y – от центра тяжести площадки опирания до точки, вокруг которой стенка опрокидывается называется:

1. Предельный момент

2. Удерживающий момент

3. Изгибающий момент

4. Крутящий момент

5. Опрокидывающий момент

8.13 Сила, равная сумме всех горизонтальных сил называется:

1. Сдвигающая сила

2. Предельная сила

3. Сила растяжения

4. Сила сжатия

5. Удерживающая сила

8.14 Сила равная сумме всех вертикальных сил умноженной на коэффициент трения подошвы фундамента по грунту называется:

1. Сдвигающая сила

2. Предельная сила

3. Сила растяжения

4. Сила сжатия

5. Удерживающая сила

8.15 Коэффициент условия работы, принимаемый для проверки на опрокидывание равен:

A) 0.7 - 0.8

B) 1.0 -1.2

C) 2,0 -2,1

D) 0,8 - 0,9

E) 3,0 -3,5

9.1 В каком разделе УМЛ отражаются вопросы состояния проблемы, которой посвящена работа, ее актуальность и необходимость?

1. На титульном листе

2. В содержании

3. Во введении

4. В списке литературы

5. В приложении

9.2 В каком порядке располагаются источники в списке литературы.

1. В произвольном порядке

2. В порядке появления в тексте или алфавитном порядке

3. В алфавитном порядке

4. В порядке появления в тексте

5. В порядке установленном структурным подразделением

9.3 При ссылке в тексте на источники следует приводить порядковый номер по списку литературы, заключенный в:

1. В квадратные или косые скобки

2. В круглые скобки

3. В фигурные скобки

4. Без скобок

5. Произвольно

9.4 Текст УМЛ и других документов следует печатать, соблюдая следующие разделы полей: правое, верхнее, нижнее – не менее:

1. 20мм

2. 30мм

3. 35мм

4. 15мм

5. 40мм

9.5 Текст УМЛ и других документов следует печатать, соблюдая следующие разделы полей: левое не менее:

1. 20мм

2. 30мм

3. 35мм

4. 15мм

5. 40мм

9.6 Абзацный отступ текста начинается не менее чем с:

1. Со второго знака

2. С третьего знака

3. С четвертого знака

4. С пятого знака

5. Произвольно

9.7 Разделы должны иметь порядковые номера в пределах всего документа обозначенные:

1. Римскими цифрами

2. Буквами русского алфавита

3. Буквами английского алфавита

4. Арабскими цифрами с точкой

5. Арабскими цифрами без точки

9.8 Страницы УМЛ следует нумеровать, по всему тексту соблюдая:

1. Римскими цифрами

2. Арабскими цифрами, соблюдая сквозную нумерацию

3. Буквами русского алфавита

4. Арабскими цифрами, не соблюдая сквозную нумерацию

5. Римскими цифрами, соблюдая сквозную нумерацию

9.9 В тексте документа значения с обозначением единиц физических величин и единиц счета следует писать:

1. Словами

2. Арабскими цифрами

3. Римскими цифрами

4. Словами с пояснением

5. Произвольно

9.10 Если в тексте документа приводят диапазон числовых значений физической величины, выраженных в одной и той же единице физической величины, то обозначение величины указывается:

1. Произвольно

2. После каждого числового значения

3. После последнего числового значения диапазона

4. Не указывается

5. Указывается при необходимости

9.11 Уравнения и формулы следует выделять из текста на отдельную строку. Выше и ниже каждой формулы или уравнения должно быть оставлено:

1. Произвольное количество строк

2. Не менее одной свободной строки

3. Пять строк и более

4. Пустые строки не оставляются

5. Данная норма не регламентируется

9.12 Формулы в УМЛ должны нумероваться сквозной нумерацией арабскими цифрами которые записывают в:

1. В квадратные или косые скобки

2. В круглые скобки

3. В фигурные скобки

4. Без скобок

5. Произвольно

9.13 Иллюстрации в УМЛ следует располагать непосредственно:

1. После текста

2. На следующей странице, в центре

3. На следующей странице, по правому краю

4. После текста или на следующей странице, в центре

5. После текста или на следующей странице, справа

9.14 Название таблицы в УМЛ следует помещать:

1. Произвольно

2. Над таблицей слева в одну строку с ее номером через тире

3. Над таблицей справа в одну строку с ее номером через тире

4. Под таблицей

5. В графах таблицы

9.15 Расстояние между нижним срезом таблицы и текстом должно быть:

1. Норма не регламентируется

2. Две пустые строки

3. Одна пустая строка

4. Произвольно

5. Пустых строк нет

10.1 Сигнальная специфика случайных процессов рассматривается :

1. в теории вероятности

2. в теории информации

3. в теории предельных состояний

4. в теории надежности

5. в теории эксперимента

10.2 Материальный носитель информации, средство перенесения информации в пространстве и времени это:

1. помехи

2. шумы

3. сигнал

4. звук

5. код

10.3 Условия, обеспечивающие установление и способствующие сохранению сигнального соответствия состояний называются:

1. помехами и шумами

2. кодом

3. сигналом

4. звуком

5. динамикой

10.4 Постороннее воздействие нарушающее сохранение сигнального соответствия называется:

1. помехами и шумами

2. кодом

3. сигналом

4. звуками

5. радиоволнами

10.5 Сигналы, являющиеся стабильными состояниями физических объектов ( книга, фотография, магнитофонная запись) называются:

1. статическими

2. кодом

3. динамическими

4. музыкальными

5. переменными

10.6 Силовые поля изменение состояния которых не может быть локализовано в неизолированной части поля и приводит к распространению возмущения называют сигналами:

1. статическими

2. кодом

3. динамическими

4. музыкальными

5. переменными

10.7 Если информационная нагрузка на каждый элемент сигнала меньше той, которую элемент способен нести то данное явление называют:

1. скоростью передачи информации

2. пропускной способностью канала

3. избыточностью

4. перегрузкой

5. недостаточностью

10.8 Количество информации передаваемое в единицу времени

1. скоростью передачи информации

2. пропускной способностью канала

3. избыточностью

4. нет правильного ответа

5. объемом

10.9 Предел выше которого увеличение скорости невозможно называют

1. скоростью передачи информации

2. пропускной способностью канала

3. избыточностью

4. деформацией

5. уровнем надежности

10.10 Способ введения избыточности, при котором обеспечивается одновременно сколь угодно малая вероятность ошибки , и конечная (отличная от нуля) скорость передачи информации, причем сколь угодно близкая к пропускной способности канала это теорема:

1. Пифагора

2. Шэннона

3. Вейерштрасса

4. Ньютона

5. Бернулли

10.11 Теория кодирования изучает:

1. способы построения отдельных кодов и их свойства

2. соответствие состояний

3. зависимости вероятностей ошибок от параметров

4. устойчивость

5. равновесие твердых тел

10.12 Объективно равные интервалы которые измеряются одинаковыми по длине отрезками независимо от места расположения предполагает шкала:

1. наименований

2. порядка

3. интервалов

4. разностей

5. отношений

10.13 Отношения двух наблюдаемых значений измеряемой величины независящих от того в какой из шкал произведены измерения называют:

1. шкалой наименований

2. шкалой порядка

3. шкалой отношений

4. шкалой разностей

5. шкалой интервалов

10.14 Циклическая или периодическая шкала интервалов называется:

1. шкалой наименований

2. абсолютная шкала

3. шкалой отношений

4. шкалой разностей

5. шкалой интервалов

10.15 Числовая ось, особенностью которой является безразмерность и абсолютность единицы называется:

1. шкалой наименований

2. абсолютная шкала

3. шкалой отношений

4. шкалой разностей

5. шкалой интервалов

11.1 Переменная значение которой расплывчато по своей природе , как метки размытого, расплывчатого множества называют:

1. математической переменной

2. лингвистической переменной

3. физической переменной

4. статической переменной

5. статистической переменной

11.2 Неопределенное число элементов принадлежность которых к множеству нельзя однозначно определить по конкретным признакам называют:

1. расплывчатым множеством

2. лингвистическим множеством

3. объединенным множеством

4. статистическим множеством

5. массивом

11.3 В теории размытых множеств задание функций принадлежности осуществляется следующими подходами:

1. Эвристический подход

2. Статистический подход

3. Частичное задание, интервальное задание кратная расплывчатость

4. Эвристический, статистический, частное задание, интервальное задание, кратная расплывчатость

5. Статический подход

11.4 В случае, если субъект определяет, как он понимает степень принадлежности является:

1. Эвристический подход

2. Статистический подход

3. Частичное задание, интервальное задание кратная расплывчатость

4. Динамический подход

5. Статический подход

11.5 В случае, если определяется усредненная функция задаваемая разными экспертами подход называют:

1. Эвристический подход

2. Статистический подход

3. Частичное задание, интервальное задание кратная расплывчатость

4. Динамический подход

5. Статический подход

11.6 Целенаправленносить деятельности. Алгоритмичность деятельности. Системность результатов деятельности это:

1. Системность практической деятельности

2. Системность познавательной деятельности

3. Системность среды, окружающей человека

4. Системность статики

5. Системность динамики

11.7 Анализ и синтез. Диалектика как метод. Системность результатов познания это:

1. Системность практической деятельности

2. Системность познавательной деятельности

3. Системность среды, окружающей человека

4. Системность статики

5. Системность динамики

11.8 Естественная системность природы. Системность человеческого общества. Системность взаимодействия человека со средой это:

1. Системность практической деятельности

2. Системность познавательной деятельности

3. Системность среды, окружающей человека

4. Системность статики

5. Системность динамики

11.9 Вспомогательное средство , объект, который в определенной ситуации заменял другой объект первоначально назывался:

1. Системностью

2. Моделью

3. Средой

4. Схемой

5. Кодом

11.10 Объект заместитель, который в определенных условиях может заменить объект оригинал, воспроизводя интерисующие нас свойства и характеристики оригинала, причем имеет существенные преимущества, удобства называется:

1. Системностью

2. Моделью

3. Средой

4. Схемой

5. Кодом

11.11 Результат отображения одной абстрактной математической структуры на другую, также абстрактную , либо как результат интерпретации первой модели в терминах и образах второй называется:

1. Системностью

2. Моделью

3. Средой

4. Схемой

5. Кодом

11.12 Способ существования знаний может быть:

1. Системностью

2. Моделью

3. Средой

4. Схемой

5. Кодом

11.13 Форма организации и представления знаний, средство соединения новых знаний с имеющимися это:

1. Познавательная модель

2. Прагматическая модель

3. Динамическая модель

4. Статическая модель

5. Статистическая модель

11.14 Средство управления, средство организации практических действий, способ представления образцово правильных действий или их результата.т.е.рабочее представление целей это:

1. Познавательная модель

2. Прагматическая модель

3. Динамическая модель

4. Статическая модель

5. Статистическая модель

11.15 Что отражают познаватальные модели:

1. Существующие цели

2. Не существующие цели

3. Желаемые цели

4. Динамические цели

5. Статистические цели

12.1 Что отражают прагматические модели:

1. Существующие цели

2. Не существующие цели

3. Желаемые цели

4. Статистические цели

5. Виртуальные цели

12.2 Средство повышения эффективности использовать которое следует осторожно по мере возрастания сложности проблемы называется:

1. Оптимизацией

2. Кибернетизацией

3. Стандартизацией

4. Механизацией

5. Автоматизацией

12.3 Является ли задача выбора частной задачей системного анализа.

1. Является

2. Не является

3. Частично является

4. Является в исключительных случаях

5. Частично является в отдельных случаях

12.4 Если проблемы системы выходят за пределы формальных математических постановок задач то их решение выполняют при помощи:

1. Экспертов

2. Численными методами

3. Методами высшей математики

4. Аудита

5. Проверки соответствия

12.5 Критика благотворно влияет на эксперта, если она психологически не связана с персональной конфронтацией - это идея метода:

1. Статистической неопределенности

2. Теории игр

3. Метода «Делфи»

4. Теоремы Гаусса

5. Закона нормальных напряжений

12.6 Системы, созданные человеком, называют:

1. Искусственными

2. Естественными

3. Субъективными

4. Природными

5. Объективными

12.7 Системы, возникшие в природе без участия человека, называют:

1. Искусственными

2. Естественными

3. Субъективными

4. Природными

5. Объективными

12.8 Идеальный образ будущего состояния системы называют:

1. Искусственной целью

2. Естественной целью

3. Субъективной целью

4. Объективной целью

5. Неопределенной целью

12.9 Будущее реальное состояние системы называют:

1. Объективной целью

2. Естественной целью

3. Субъективной целью

4. Искусственной целью

5. Неопределенной целью

12.10 Система есть средство достижения цели это:

1. Первое определение системы

2. Второе определение системы

3. Модель «черного ящика»

4. Уравнение системы

5. Модель системы

12.11 Цель – в произвольный момент указать время . Это система:

1. Телевидения

2. Пекарни

3. Городского транспорта

4. Часов

5. Модема

12.12 Цель – обеспечить выпечку хлеба в заданном ассортименте. Это система:

1. Телевидения

2. Пекарни

3. Городского транспорта

4. Часов

5. Модема

12.13 Цель – передать зрительную информацию в звуковом сопровождении. Система:

1. Телевидение

2. Пекарня

3. Городской транспорт

4. Часы

5. Модем

12.14 Цель – обеспечить быстрое передвижение людей в пределах города. Система:

1. Телевидение

2. Пекарня

3. Городской транспорт

4. Часы

5. Модем

12.15 Целостность и обособленность от среды обеспечивает модель:

1. Телевидения

2. Черного ящика

3. Прозрачного ящика

4. Часов

5. Модемa

13.1 Система есть совокупность взаимосвязанных элементов, обособленная от среды и взаимодействующая с ней как целое.

1. Первое определение системы

2. Второе определение системы

3. Модель «черного ящика»

4. Модель модема

5. Модель прозрачного ящика

13.2 Системы, в которых происходят какие бы то ни было изменения со временем называют:

1. Временными

2. Статическими

3. Статистическими

4. Динамическими

5. Постоянными

13.3 Действие, придающее всей деятельности целенаправленность называется:

1. Выбором

2. Совокупностью целей

3. Критерием предпочтения

4. Оценкой альтернативы

5. Идеей

13.4 Принятие решения как действия над множеством альтернатив, в результате которого подмножество выбора альтернатив называется:

1. Выбором

2. Совокупностью целей

3. Критерием предпочтения

4. Оценкой альтернативы

5. Совокупностью идей

13.5 Сравнение альтернатив по одному или нескольким критериям, которые имеют как количественный так и качественный характер называется:

1. Выбором

2. Совокупностью целей

3. Критерием предпочтения

4. Оценкой альтернативы

5. Экспертными системами

13.6 Язык, при котором каждую конкретную альтернативу можно оценить конкретным числом называется:

1. Критериальным языком описания выбора

2. Языком бинарных отношений

3. Языком функций выбора

4. Иностранным языком

5. Национальным языком

13.7 При рассмотрении альтернатив в паре пользуются языком:

1. Критериальным языком описания выбора

2. Языком бинарных отношений

3. Языком функций выбора

4. Иностранным языком

5. Национальным языком

13.8 Язык, который позволяет сделать выбор как операцию над произвольным множеством, которая ставит этому множеству в соответствие некоторое его подмножество называют:

1. Критериальным языком описания выбора

2. Языком бинарных отнощений

3. Языком функций выбора

4. Иностранным языком

5. Национальным языком

13.9 В теории игр точка равновесия интересов сторон называется:

1. Точкой сожаления

2. Точкой пессимизма

3. Седловой точкой

4. Точкой отсчета

5. Точкой равновесия

13.10 Критерий выбора «наименьшего из зол называют»:

1. Минимаксным критерием

2. Критерием пессимизма

3. Максиминным критерием

4. Критерием Гурвица

5. Критерием Пифагора

13.11 Максиминным критерием называют:

1. Критерий выбора «наименьшего из зол называют»

2. Комбинации наилучшего и наихудшего исходов

3. Критерий выбора через проигрыш

4. Критерий Гурвица

5. Критерием Пифагора

13.12 Минимаксным критерием называют:

1. Критерий выбора «наименьшего из зол называют»

2. Комбинации наилучшего и наихудшего исходов

3. Критерий выбора через проигрыш

4. Критерий Гурвица

5. Критерием Пифагора

13.13 Критерием Гурвица называют:

1. Критерий выбора «наименьшего из зол называют»

2. Комбинации наилучшего и наихудшего исходов

3. Критерий выбора через проигрыш

4. Критерий минимального сожаления

5. Критерием Пифагора

13.14 При выборе в условиях неопределенности взаимодействующие стороны называются:

1. Партнерами

2. Игроками

3. Противниками

4. Болельщиками

5. Экспертами

13.15 При выборе в условиях неопределенности выбираемые альтернативы называются:

1. Ходами

2. Шагами

3. Решением

4. Системами

5. Кодом

14.1 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия грунта обратной засыпки, если высота стенки Н = 2,4 м, давление грунта Р=13,7 кн/м²

1. 16,44 кн/м

2. 20,0 кн/м

3. 19,32 кн/м

4. 25,05 кн/м

5. 30,62 кн/м

14.2 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия грунта обратной засыпки, если высота стенки Н = 2,8 м, давление грунта Р=13,8 кн/м²

1. 16,44 кн/м

2. 20,0 кн/м

3. 19,32 кн/м

4. 25,05 кн/м

5. 30,62 кн/м

14.3 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия грунта обратной засыпки, если высота стенки Н = 3,0 м, давление грунта Р=20,0 кн/м²

1. 16,44 кн/м

2. 20,0 кн/м

3. 19,32 кн/м

4. 25,05 кн/м

5. 30,0 кн/м

14.4 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия временной нагрузки, если высота стенки Н = 3,0 м, величина временной нагрузки Рq = 21 кн/м²

1. 16,44 кн/м

2. 20,0 кн/м

3. 19,32 кн/м

4. 63 кн/м

5. 30,0 кн/м

14.5 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия временной нагрузки, если высота стенки Н = 6,0 м, величина временной нагрузки Рq = 18 кн/м²

1. 16,44 кн/м

2. 108 кн/м

3. 19,32 кн/м

4. 63 кн/м

5. 30,0 кн/м

14.6 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия временной нагрузки, если высота стенки Н =5,0 м, величина временной нагрузки Рq = 10 кн/м²

1. 16,44 кн/м

2. 108 кн/м

3. 50 кн/м

4. 63 кн/м

5. 30,0 кн/м

14.7 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия грунтовой воды, если высота слоя грунтовой воды h=1.2 м, давление грунтовой воды Р₁=10,287 кн/м²

1. 6,17 кн/м

2. 8,12 кн/м

3. 10 кн/м

4. 5,32 кн/м

5. 11,0 кн/м

14.8 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия грунтовой воды, если высота слоя грунтовой воды h=1.1 м, давление грунтовой воды Р₁=11.0 кн/м²

1. 6,17 кн/м

2. 6,05 кн/м

3. 10 кн/м

4. 5,32 кн/м

5. 11,0 кн/м

14.9 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия грунтовой воды, если высота слоя грунтовой воды h=1.3 м, давление грунтовой воды Р₁=8.0 кн/м²

1. 6,17 кн/м

2. 6,05 кн/м

3. 10 кн/м

4. 5,2 кн/м

5. 11,0 кн/м

14.10 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия воды в реке, если уровень воды в реке h=1.0 м, давление воды Р2=10.0 кн/м²

1. 6,17 кн/м

2. 6,05 кн/м

3. 10 кн/м

4. 5,0 кн/м

5. 11,0 кн/м

14.11 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия воды в реке, если уровень воды в реке h=1.1 м, давление воды Р₂=10.0 кн/м²

1. 6,17 кн/м

2. 6,05 кн/м

3. 10 кн/м

4. 5,5 кн/м

5. 11,0 кн/м

14.12 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия воды в реке, если уровень воды в реке h=1.2 м, давление воды Р₂=10.0 кн/м²

1. 6,17 кн/м

2. 6,05 кн/м

3. 10 кн/м

4. 6,0 кн/м

5. 11,0 кн/м

14.13 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия взвешенного грунта в реке, если уровень взвешенного грунта в реке h=1.285 м, давление взвешенного грунта Р₃=0,3 кн/м²

1. 6,17 кн/м

2. 6,05 кн/м

3. 0,12кн/м

4. 0,19 кн/м

5. 0,15 кн/м

14.14 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия взвешенного грунта в реке, если уровень взвешенного грунта в реке h=1.1 м, давление взвешенного грунта Р₃=0,3 кн/м²

1. 6,17 кн/м

2. 6,05 кн/м

3. 0,12кн/м

4. 0,19 кн/м

5. 0,165 кн/м

14.15 Определить величину равнодействующей силы на единицу длины подпорной стенки, от воздействия взвешенного грунта в реке, если уровень взвешенного грунта в реке h=0,9м, давление взвешенного грунта Р₃=0,3 кн/м²

1. 6,17 кн/м

2. 6,05 кн/м

3. 0,12кн/м

4. 0,135 кн/м

5. 0,165 кн/м

15.1 Определить величину М_упр в сечении если R_a=5,01 кН, x=2 м

1. 8, 51 кНм

2. 10,02 кНм

3. 9, 33 кНм

4. 12, 71 кНм

5. 11, 17 кНм

15.2 Определить величину М_упр в сечении если R_a=4,58 кН, x=2 м

1. 8,53 кНм

2. 13,67 кНм

3. 9,16 кНм

4. 12,71 кНм

5. 13,95 кНм

15.3 Определить величину М_упр в сечении если R_a=4,58 к, x=1,5 м

1. 6,87 кНм

2. 7,02 кНм

3. 5,36 кНм

4. 4,58 кНм

5. 30,4 кНм

15.4 Определить величину М_упр в сечении если R_a=4,58 кН, x=2,5 м

1. 12,8 кНм

2. 2,5 кНм

3. 4,58 кНм

4. 10,46 кНм

5. 11,45 Кнм

15.5 Определить величину М_упр в сечении если R_a=6,17 кН, x=3

1. 8,2 кНм

2. 18,51 кНм

3. 15,64 кНм

4. 20,8 КНм

5. 14,0 кНм

15.6 Определить величину М_упр в сечении если R_a=6,17 кН, x=1,5 м

1. 7,4 кНм

2. 8,52 кНм

3. 10,6 кНм

4. 9,255 кНм

5. 10,8 кНм

15.7 Определить величину М_упр в сечении если R_a=3,17 кН, x=1,5 м

1. 4,75 кНм

2. 2,62 кНм

3. 3,58 кНм

4. 9,74 кНм

5. 4,00 кНм

15.8 Определить величину М_упр в сечении если R_a=4,17 кН, x=3 м

1. 10,4 кНм

2. 11,8 кНм

3. 13,2 кНм

4. 8,64 кНм

5. 12,51 кНм

15.9 Определить величину М_упр в сечении если R_a=6,8 кН, x=3 м

1. 18,7 кНм

2. 15,43 кНм

3. 22,1 кНм

4. 19,71 кНм

5. 20,40 кНм

15.10 Определить величину М_упр в сечении если R_a=6,8 кН, x=2 м

1. 15,7 кНм

2. 12,3 кНм

3. 13,6 кНм

4. 10,51 кНм

5. 7,83 кНм

15.11 Определить величину Q_упр в сечении если R_a=6,8 кН, x=1,5 м

1. 1,5 кН

2. 7,8 кН

3. 6,8 кН

4. 15 кН

5. 3,4 кН

15.12 Определить величину Q_упр в сечении если R_a=5 кН, x=2 м

1. 2,0 кН

2. 4,6 кН

3. 6,0 кН

4. 2,5 кН

5. 5,0 кН

15.13 Определить величину Q_упр в сечении если R_a=7,8 кН, x=3 м

1. 7,8 кН

2. 2,5 кН

3. 10,3 кН

4. 7,0 кН

5. 5,0 кН

15.14 Определить величину Q_упр в сечении если R_a=4,8 кН, x=1,5 м

1. 3,5 кН

2. 4,8 кН

3. 5,7 кН

4. 5,0 кН

5. 3,0 кН

15.15 Определить величину Q_упр в сечении если R_a=3,7 кН, x=2 м

1. 3,5 кН

2. 5,4 кН

3. 3,7 кН

4. 5,0 кН

5. 2,0 кН