Билет 13

Задание 1.

Составить программу, которая печатает true, если точка с координатами (x,y) принадлежит заштрихованной области, и false в противном случае:

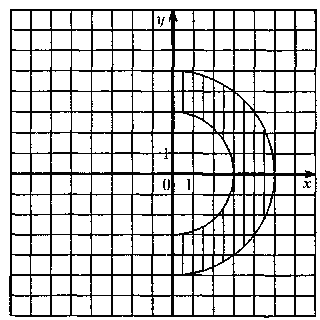
Вопросы:

1. Сформулируйте методические цели решения этой задачи.

2. Постройте систему вопросов к учащимся по поиску решения задачи.

3. Используя учебные пособия, подберите задачи, подобные данной задаче.

4. Начертите блок-схему алгоритма решения этой задачи.

Задание 2.

Используя среду программирования (например, Turbo Pascal), вычислить методом Монте-Карло число π = 3,141592653, проведя 100000, 1000000 и 10000000 испытаний (выборов случайной точки), качественно проанализировать результаты.

Вычисление числа π методом Монте-Карло

Используем построенную модель определения площади круга для приближенного вычисления числа π методом Монте-Карло.

Компьютерная модель для приближенного вычисления числа π , при r=1

Программа, представляющая математическую модель вычисления числа π методом Монте-Карло записанная на языке программирования Паскаль:

Program MonteKarlo;

var x,y,s1: real;

n1,n,i:longint;

begin

writeln ('Введите количество точек n=');

readln(n);

randomize;

n1:=0;

for i:=1 to n do

begin

x:=2*random;

y:=2*random;

if sqr(x-1)+sqr(y-1)<=1 then

n1:=n1+1;

end;

S1:=(4*n1)/n;

writeln ('Значение s1=');

readln;

end.

Результаты вычисления числа π :

	N=100	N=1000	N=10000	Точное значение
Число Пи	3,08	3,06	3,1256	3,141593

Вывод: Если сравнить полученные результаты, при N=100, N=1000, N=10000, то можно заметить, что π приблизительно равно истинному значению. Результаты тем точнее, чем большее количество точек задается.

Вопросы:

1. Какова суть метода Монте-Карло?

2. Какие факторы влияют на результат данной задачи.

Ответы на вопросы:

1. Алгоритм метода статистических испытаний (метод Монте-Карло):

S_кр/ S_кв = N₁/ N → S_кр = 4N₁/ N = π.

1) Формирование последовательности равномерно распределенных случайных величин.

2) Преобразование полученной последовательности случайных величин с заданными вероятностными характеристиками.

3) Вычисление реакции объекта на случайные воздействия.

4) Обработка статистических данных.

2. Факторы влияющие на результат данной задачи:

- число N случайных точек,

- число испытаний

Приложение:

Рассмотрим круг радиуса r = 1 с центром в точке (1;1). Круг вписан в квадрат площадью 4 ед. Выбираем внутри квадрата n – случайных точек, т .е. задаем координаты точек х, у, 0 ≤ х ≤2, 0 ≤ у ≤ 2.

N₁ – число точек, попавших внутрь круга.

N – общее число точек, которое мы задаем.

Выходные данные: S_кр = π*r² = π (r = 1).

Условия попадания точки в круг: (х – 1)² + (у – 1)² ≤ 1.