Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

ГОУ ВПО «УГТУ - УПИ имени первого Президента России Б.Н. Ельцина»

Частотные характеристики резонансных цепей

Методические указания к лабораторной работе № 6

по курсам «Основы теории цепей», «Теория электрических цепей»

для студентов направлений «Радиотехника», «Телекоммуникации», «Информационная безопасность»

Екатеринбург 2008

Составители Е.В. Вострецова, Ю.В. Шилов

Научный редактор доц., канд. техн. наук А.П. Мальцев

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ РЕЗОНАНСНЫХ ЦЕПЕЙ: Методические указания к лабораторной работе № 5 по курсам «Основы теории цепей», «Теория электрических цепей» /Е. В. Вострецова, Ю.В. Шилов. Екатеринбург, УГТУ-УПИ, 2008г.

Указания включают в себя описание лабораторной работы, посвященной исследованиям частотных характеристик резонансных цепей - простого и сложного колебательных контуров.

Описания работ содержат краткие сведения из теории, задания для выполнения расчетной части, методики проведения эксперимента, рекомендации по оформлению отчета.

Библиогр.: 5 назв. Рис.4

Подготовлено кафедрой “Теоретические основы радиотехники”.

© УГТУ-УПИ, 2008

1. Цель работы

Практическое знакомство с частотными характеристиками резонансных цепей. Экспериментальная проверка правильности соотношений, описывающих характеристики простого и сложного колебательных контуров.

2. Основные теоретические положения

В теории цепей используют следующее определение резонанса: резонанс – это такой режим работы электрической цепи, содержащей емкости и индуктивности, при котором реактивные составляющие входных сопротивления и проводимости цепи равны нулю.. На резонансной частоте входные сопротивление и проводимость электрической цепи имеют чисто резистивный характер, а входной ток цепи совпадает по фазе с приложенным напряжением.

Простейшей электрической цепью, в которой наблюдается явление резонанса, является одиночный колебательный контур, представляющий собой замкнутую цепь, состоящую из конденсатора и индуктивной катушки. В зависимости от способа подключения источника энергии, различают

• последовательный колебательный контур (источник энергии включен последовательно с конденсатором и индуктивной катушкой)

• параллельный колебательный контур (источник энергии подключен параллельно реактивным элементам).

Для расчета параллельного колебательного контура часто используют эквивалентную схему, в которой индуктивная катушка представлена последовательной схемой замещения (рис. 6.1).

i_вх(t)

R_L

u_вых(t)

С₂

L₃

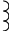
Рис. 6.1. Схема замещения простого параллельного контура

Комплексное входное сопротивление параллельного колебательного контура, в соответствии с рис. 6.1, равно:

Ограничимся, случаем, когда частота внешнего воздействия близка к резонансной и элементы контура имеют высокую добротность (_pL >> R). Тогда

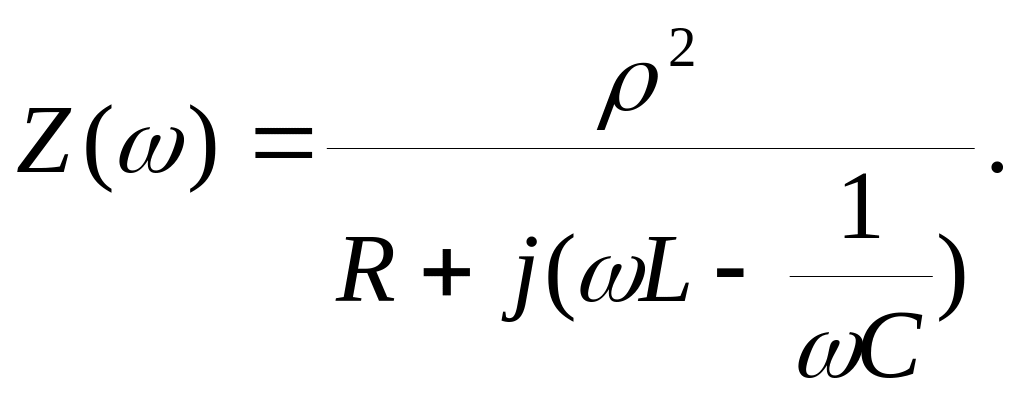
Здесь  - характеристическое сопротивление последовательного колебательного контура, составленного из тех же элементов, что и рассматриваемый параллельный колебательный контур.

На резонансной частоте мнимая составляющая комплексного входного сопротивления контура должна быть равна нулю, что возможно только при

L – 1/C = 0.

Условие резонанса токов в параллельном колебательном контуре, при высокой добротности элементов, имеет такой же вид, как условие резонанса напряжений в последовательном колебательном контуре, и, следовательно, частота резонанса токов совпадает с резонансной частотой последовательного колебательного контура, составленного из тех же элементов:

На резонансной частоте

• входное сопротивление контура (резонансное сопротивление) имеет чисто резистивный характер и равно:

Z(₀) = ²/R;

• действующие значения токов ветвей контура одинаковы:

I_С = I_L = U ;

где U — действующее значение напряжения на контуре;

• добротность

Важнейшая особенность последовательного колебательного контура заключается в том, что амплитуда реакции контура на гармоническое воздействие существенно зависит от частоты. На резонансной частоте и в узком диапазоне частот около нее амплитуда отклика достигает наибольшего значения; на частотах, значительно отличающихся от резонансной, амплитуда отклика во много раз меньше максимального значения. Если на вход такого контура подать сумму гармонических колебаний различных частот, имеющих одинаковую амплитуду, то на выходе можно обнаружить, что амплитуда колебаний, частота которых близка к резонансной, значительно превышает амплитуду колебаний, частота которых отличается от резонансной. Контур как бы «пропускает» колебания одних частот и «не пропускает» колебания других частот. Способность электрической цепи выделять колебания отдельных частот из суммы колебаний различных частот называется избирательностью.

В идеальном случае отклик избирательной цепи должен иметь постоянное значение в пределах определенного диапазона частот, называемого полосой пропускания цепи, и быть равным нулю за пределами этого диапазона. АЧХ реальных избирательных цепей, в том числе и АЧХ последовательного колебательного контура, отличаются от характеристик идеальной избирательной цепи отсутствием резкой границы между диапазонами пропускаемых и задерживаемых (подавляемых) частот. Очевидно, избирательные свойства реальных цепей будут тем выше, чем ближе к прямоугольной будет форма их нормированной АЧХ.

Полоса пропускания реальных избирательных устройств условно определяется как диапазон частот, в пределах которого амплитуда отклика цепи не падает ниже уровня = 0,707 от максимального значения. На частотах, соответствующих границам полосы пропускания, амплитуда отклика составляет 0,7 от максимального значения, а потребляемая цепью активная мощность в 2 раза меньше максимальной.

Избирательные свойства колебательного контура определяются формой нормированной АЧХ.

Верхняя и нижняя граничные частоты:

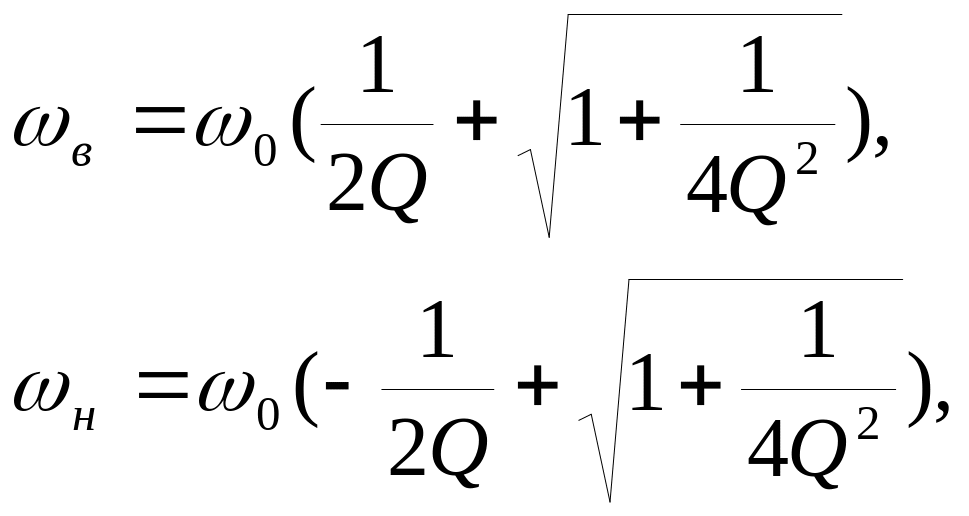
Ширина полосы пропускания пропорциональна резонансной частоте контура

2 = _в – _н = ₀/Q.

Таким образом, избирательные свойства последовательного колебательного контура зависят от его добротности: чем выше добротность контура, тем меньше ширина полосы пропускания.

Пусть контур питается от источника тока с конечным внутренним сопротивлением R_i.

Учесть влияние сопротивления источника, подключенного параллельно емкости, можно преобразовав параллельное соединение в последовательное. Параллельные схемы замещения элементов при высокой добротности элементов содержат элементы:

С_пар = С_посл = С,

L_пар = L_посл=L,

На частотах, близких к резонансной, внесенные в контур сопротивления

R_i2' = R_i3'=² /R_i = R_i'.

Влияние R_i' на параметры контура аналогично влиянию шунта, т. е. с увеличением R_i' снижается эквивалентная добротность контура и ухудшается его избирательность:

,

Следовательно, для увеличения эквивалентной добротности контура и улучшения его избирательности необходимо, чтобы сопротивление нагрузки контура R_i было бы как можно большим, т. е. чтобы был обеспечен режим работы, близкий к режиму холостого хода.

На практике широко применяются колебательные контуры с неполным включением реактивного элемента – с неполным включением индуктивности и с неполным включением ёмкости. На рис. 6.2. показан контур с неполным включением индуктивности.

Рис. 6.2. Контур с неполным включением индуктивности.

Для характеристики «неполноты» включения реактивного элемента используется коэффициент включения:

Коэффициент включения изменяется в пределах от нуля до единицы. В последнем случае рассматриваемый колебательный контур вырождается в параллельный колебательный контур основного вида.

В связи с тем, что одна из ветвей параллельного колебательного контура с неполным включением реактивного элемента представляет собой последовательное включение конденсатора и индуктивной катушки, в контуре этого вида наряду с резонансом токов имеет место резонанс напряжений.

Конструктивной особенностью колебательного контура с неполным включением индуктивности является наличие в нем индуктивной катушки с отводом или со скользящим контактом, разделяющим катушку на две секции

При высокой добротности элементах на частотах, близких к резонансной, входное сопротивление может быть определено по приближённой формуле:

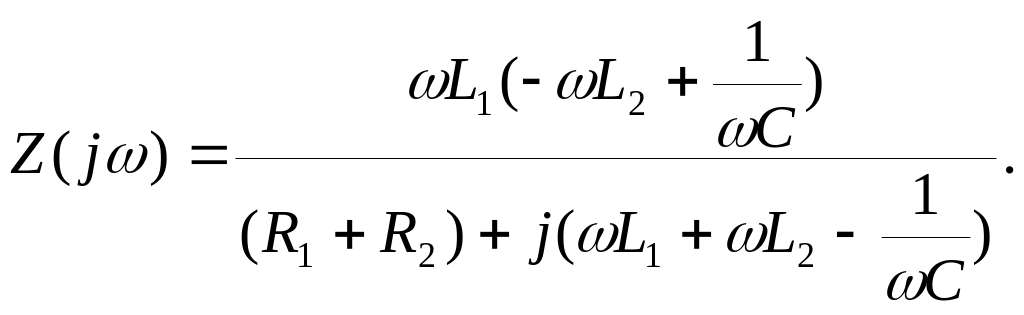
На частоте резонанса токов мнимая составляющая Z (j) должна равняться нулю, что выполняется при:

L₁ + L₂ – 1/C = 0.

Следовательно,

Таким образом, частота резонанса токов параллельного колебательного контура не зависит от коэффициента включения индуктивности и совпадает с резонансной частотой последовательного колебательного контура, построенного из тех же элементов, что и рассматриваемый колебательный контур.

Частота резонанса напряжений ₀ определяется только индуктивностью второй ветви L₂ и, следовательно, зависит от коэффициента включения индуктивности:

С уменьшением коэффициента включения индуктивности частота ₀ уменьшается, оставаясь большей, чем _p.

Cопротивление рассматриваемого контура на частоте резонанса токов:

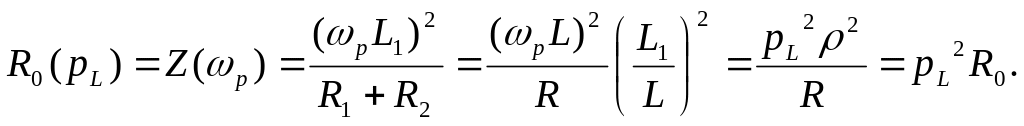
Здесь R = R₁ + R₂ - суммарное сопротивление потерь,

 - характеристическое сопротивление рассматриваемого контура, равное характеристическому сопротивлению последовательного колебательного контура, составленного из тех же элементов,

R₀ = ²/R — резонансное сопротивление параллельного контура основного вида.

Таким образом, резонансное сопротивление контура с неполным включением индуктивности R₀ (p_L) зависит от коэффициента включения и меньше, чем резонансное сопротивление контура основного типа R₀.

Амплитудно-частотная и фазо-частотная характеристики параллельного колебательного контура с неполным включением индуктивности приведены на рис. 6.3. На частотах ниже _p входное сопротивление контура определяется в основном сопротивлением ветви 1 и имеет резистивно-индуктивный характер. На частоте резонанса токов сопротивление контура достигает максимального значения R₀ (p_L) и имеет резистивный характер. На частотах выше _p сопротивление контура определяется в основном параметрами ветви 2, причем при _p <  <₀ сопротивление контура имеет резистивно-емкостной характер, а на частотах выше частоты резонанса напряжений резистивно-индуктивный. На частоте резонанса напряжений входное сопротивление контура имеет резистивный характер и достигает минимального значения, определяемого сопротивлением потерь второй ветви.

Рис. 6.3. АЧХ и ФЧХ входного сопротивления параллельного контура с неполным включением индуктивности.

Добротность параллельного колебательного контура с неполным включением индуктивности не зависит от коэффициента включения и равна добротности последовательного колебательного контура, составленного из тех же элементов.