
- •Физическая величина, измерения, единство измерений.
- •Погрешность измерений.
- •Основное уравнение измерений
- •Размер физической величины.
- •Международная система единиц 'си'.
- •10 Эталоны, как средство измерения.
- •11. Классификация измерений по способу получения информации.
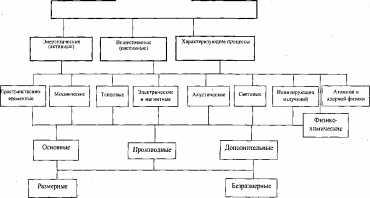
- •Классификация измерений по характеру изменения получаемой информации.
- •Источники погрешности результатов измерений.
Размер физической величины.
Размер физической величины — это количественное содержание в данном объекте свойства, соответствующего понятию “физическая величина”. Например, каждое тело обладает определенной массой, вследствие чего тела можно различать по их массе, т. е. по размеру интересующей нас ФВ.
 Значение
физической величины
получают в результате ее измерения
или вычисления в соответствии с основным
уравнением измерения Q=
q[Q\,
связывающим между собой значение ФВ Q,
числовое
значение q
и выбранную для измерения единицу [Q]. В
зависимости от размера единицы будет
меняться числовое значение ФВ, тогда
как размер ее будет оставаться неизменным.
Значение
физической величины
получают в результате ее измерения
или вычисления в соответствии с основным
уравнением измерения Q=
q[Q\,
связывающим между собой значение ФВ Q,
числовое
значение q
и выбранную для измерения единицу [Q]. В
зависимости от размера единицы будет
меняться числовое значение ФВ, тогда
как размер ее будет оставаться неизменным.
Размер единиц ФВ устанавливается законодательно путем закрепления определения метрологическими органами государства.
5 Виды физических величин. Вид уравнений, связывающие между собой различные физические величины
6 Шкалы измерений
В соответствии с логической структурой проявления свойств различают пять основных типов шкал измерений.
Шкала наименований (шкала классификации). Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности. Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами ФВ. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен.
Шкала порядка (шкала рангов). Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка. Он^ является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. ле\шя свойства, то для него может быть построена шкала порядка. Он^ является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить, во сколько раз больше или меньше конкретные проявления свойства.
Шкала интервалов (шкала разностей). Эти шкалы являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало — нулевую точку. К таким шкалам относится летосчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо Рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.
Шкала отношений. Эти шкалы описывают свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода — аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). Их примерами являются шкала массы (второго рода), термодинамической температуры (первого рода).
Шкалы отношений — самые совершенные. Они описываются уравнением Q = q[Q\, где Q — ФВ, для которой строится шкала; [Q] — ее единица измерения; д — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = qx [(?,]/ [Q2].
Абсолютные шкалы. Под абсолютными понимают шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Такие шкалы соответствуют относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.
7. Истинное значение величины и действительное.
8. Погрешность результатов измерений. Точность измерений
Погрешность измерения Дхиам — это отклонение результата измерения х от истинного (действительного) хи(хл) значения измеряемой величины:
Л*изм=*-*д-
В зависимости от формы выражения различают абсолютную, относительную и приведенную погрешности измерения.
Абсолютная погрешность определяется как разность Л = х-х или А = х~х. а относительная — как отношение
5 = ±—100% или 5 = +—100%.
Среднее арифметическое из ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого определенного измерения. Это отражает и формула (2.4), определяющая фундаментальный закон теории погрешностей. Из него следует, что если необходимо повысить точность результата (при исключенной систематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если требуется увеличить точность в 3 раза, то число измерений увеличивают в 9 раз и т. д.
Нужно четко разграничивать применение о- и ах: величина о- используется при оценке погрешностей окончательного результата, а ах — при оценке погрешности метода измерения.
В зависимости от характера проявления, причин возникновения и возможностей устранения различают систематическую и случайную составляющие погрешности измерений, а также грубые погрешности (промахи).
Систематическая Ас составляющая остается постоянной или закономерно изменяется'при повторных измерениях одного и того же параметра.
Случайная А составляющая изменяется при повторных измерениях одного и того жёГпараметра случайным образом.
Грубые погрешности (промахи) возникают из-за ошибочных дей- ствий оператора, неисправности СИ или резких изменений условий измерений. Как правило, грубые погрешности выявляются в результате обработки результатов измерений с помощью специальных критериев.
Случайная и систематическая составляющие погрешности измерения проявляются одновременно, так что общая погрешность при их независимости А = А +Д /или через СКО оА = /Од +о? .
„ -с ■■■■■.и V ' л
значение случайной погрешности заранее неизвестно, оно возникает из-за множества неуточненных факторов.
Случайные погрешности нельзя исключить полностью, но их влияние может быть уменьшено путем обработки результатов измерений. Для этого должны быть известны вероятностные и статистические характеристики (закон распределения, закон математического ожидания, СКО, доверительная вероятность и доверительный интервал). Часто для предварительной оценки законараспределения параметра используют относительную величину СКО — коэффициент вариации:
