Роздiл іі мандельштам-бріллюенівське розсіювання світла

2.1. Розсіювання Мандельштама – Бріллюена.

Розсіюванням світла називається явище, яке полягає в тому, що взаємодія середовища зі світловим пучком приводить до появи електромагнітного випромінювання того ж чи іншого спектрального складу в напрямках, що відрізняються від первинного. Воно обумовлене неоднорідністю середовища і взаємодією світла з частинками речовини, при якій міняються просторовий розподіл інтенсивності, частотний спектр і поляризація світла.

Розсіювання так як і дифракція світла залежить від розмірів неоднорідностей і довжини хвилі. Але дифракція зумовлена інтерференцією вторинних хвиль, які утворюються на неоднорідностях, а розсіювання – додаванням хвиль, які виникають при збудженні вимушених коливань електронів у неоднорідностях під дією світла [22].

Розглянемо взаємодію плоскої світлової хвилі зі звуковою хвилею (рис.2.1). Нехай у середовищі поширюється плоска звукова хвиля зі швидкістю V_а . Під кутом φ/2 до акустичної хвилі поширюється світлова хвиля 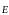_1ʲ з частотою ω₁ (довжиною хвилі в середовищі λ₁). Оскільки показник заломлення речовини залежить від густини, а отже, і від тиску, то акустична хвиля модулює показник заломлення речовини. У речовині утворюється фазова дифракційна решітка, яка рухається зі швидкістю звуку.

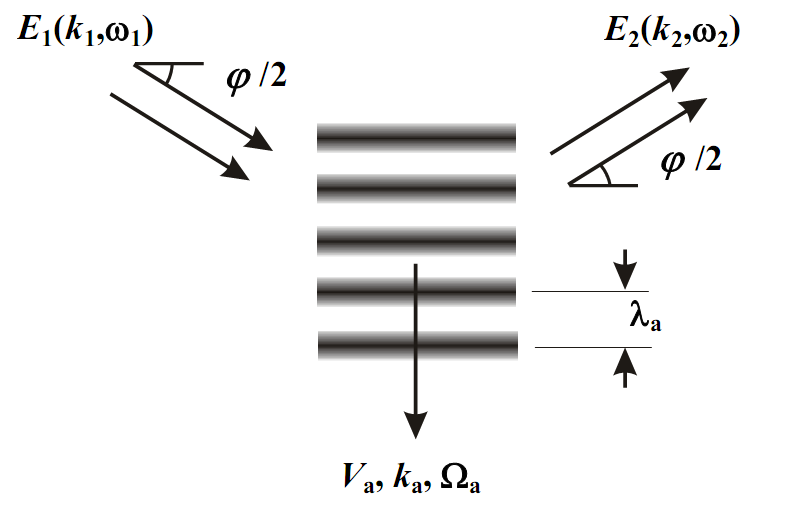
Рис. 2.1. Розташування звукової та світлових хвиль.

Утворена акустичною хвилею динамічна дифракційна решітка представляє собою систему паралельних площин, відстань між якими дорівнює довжині акустичної хвилі λ_а. На цій решітці відбувається дифракція світлової хвилі ₁, у результаті чого виникає нова плоска світлова хвиля ₂, яка спрямована згідно з правилом дзеркального відбивання від паралельних площин дифракційної решітки. Розглянута ситуація нагадує відбивання рентгенівських променів від атомних площин у кристалах, коли напрям відбивання знаходять із застосуванням відомої умови Вульфа – Брегга. Ефективне відбивання світла від системи паралельних площин відбувається при виконанні умови Вульфа – Брегга при N = 1:

(2.1)

Оскільки дифракційна решітка (система площин) рухається зі швидкістю звуку, то завдяки ефекту Допплера спостерігається зсув частоти дифрагованої хвилі на величину

_, (2.2)

де – проекція вектора швидкості звукової хвилі на напрям поширення світла, c – швидкість світла в середовищі. З урахуванням (2.1) шляхом нескладних алгебраїчних перетворень отримаємо ∆ω = − Ω_а, де Ω_а – частота акустичної хвилі. Якщо на рис. 2.1 напрям поширення акустичної хвилі змінити на протилежний, то частота розсіюваного світла ω₂ буде більшою за частоту падаючого світла, тобто ∆ω = Ω_а.Таким чином, при розсіюванні плоскої світлової хвилі на плоскій акустичній хвилі відбувається зміна частоти світла на величину частоти звуку, а напрям розсіяння визначається умовою (2.1) [23].

При ненульовій температурі в будь-якій речовині (у твердому тілі, рідині, газі) відбуваються теплові флуктуації густини, а отже, і флуктуації діелектричної проникності та показника заломлення. Ці флуктуації можна представити як сукупність плоских акустичних хвиль, що поширюються в різних напрямках і мають різні частоти в широкому діапазоні. А на акустичних хвилях, як було показано вище, світло розсіюється. Таким чином, при ненульовій температурі в середовищі може спостерігатись розсіювання світла на флуктуаціях густини (на акустичних хвилях). Це явище називається розсіювання Мандельштама – Бріллюена (РМБ) рис. 2.2. РМБ було передбачено теоретично Л. Брілюеном (L. Brillouin) у 1922 р. та незалежно Л. І. Мандельштамом у 1926р. Експериментально РМБ вперше спостерігали Л. І. Мандельштам, Г. С. Ландсберг та Є. Ф. Гросс у 1930 р.

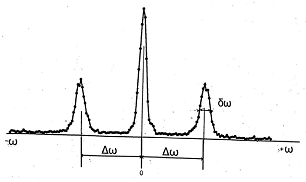
Рис. 2.2. Зміщення компонент Мандельштама – Бріллюена відносно центральної (релеївської) лінії.

Оскільки акустичні хвилі, що виникають завдяки тепловим флуктуаціям густини, поширюються у різних напрямках і мають різні і частоти, то серед цих численних біжучих дифракційних решіток завжди знайдеться така решітка з відповідним періодом, що забезпечить відбивання світла в будь-якому обраному напрямку спостереження. Таким чином, РМБ відбувається в усіх напрямках і не має якогось виділеного напрямку [24].

З квантово-механічної точки зору розсіювання Мандельштама – Бріллюена можна розглядати як розсіювання фотонів на акустичних фононах. Можливі два варіанти: стоксове та антистоксове розсіювання. При стоксовому розсіюванні відбувається народження акустичного фонона, при антистоксовому розсіюванні – зникнення фонона. При розсіюванні виконуються закони збереження енергії та імпульсу:

ħω₁ = ħω₂ ± ħΩₐ; (2.3)

ħ ₁ = ħ ± ħ _, (2.4)

де індекс "1" відповідає падаючій хвилі, індекс "2" – розсіяній хвилі, індекс "а" – акустичній хвилі.

Оскільки Ω_a << _1,2 , то ω₂ мало відрізняється від ω₁. Як наслідок, абсолютна величина хвильового вектора світлової хвилі при розсіюванні змінюється мало ǀ ₁ǀ ≈ ǀ ₂ǀ = ǀ ǀ . Розглянемо векторну діаграму (рис. 2.3), що ілюструє закон збереження імпульсу при РМБ. Хвильові вектори на діаграмі утворюють рівнобічний трикутник.

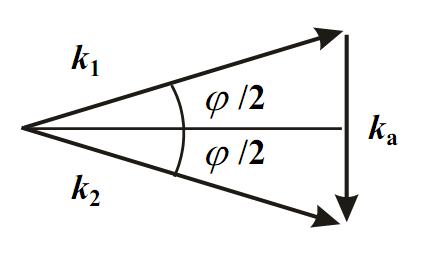
Рис. 2.3. Трикутник хвильових векторів при РМБ.

З геометричних міркувань є очевидним, що

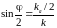, (2.5)

звідки випливає щойно розглянута умова Вульфа – Брегга (2.1). Тепер стає зрозумілим, чому N = 1 у виразі (2.1). Якщо N >1 , це відповідає випадку розсіювання фотона з народженням/зникненням N фононів. Такі багатофононні процеси малоймовірні і в подальшому розгляді вони враховуватись не будуть.

Розглянемо схему спостереження РМБ (рис. 2.4). Як уже відзначалося, РМБ можна спостерігати під різними кутами . Залежно від кута у розсіюванні будуть брати участь різні фонони (фонони з різними значеннями ). В розсіюванні на заданий кут візьме участь не будь-який фонон, а лише такий, хвильовий вектор значення якого задовольняє умові збереження імпульсу (2.4). Таким чином, в розсіюванні на маленькі кути (розсіювання "вперед") беруть участь фонони з маленькими ǀ _аǀ. Якщо закон дисперсії Ω_а(k_а) для фононів близький до лінійного (як це має місце у випадку акустичних фононів), то в розсіянні на маленькі кути братимуть участь лише низькочастотні фонони. Відповідно, при розсіянні на великі кути актуальними будуть високочастотні фонони.

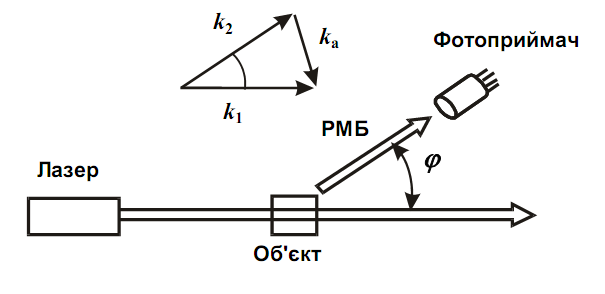
Рис. 2.4. Схема спостереження РМБ.

Таким чином, спектр розсіяного світла при РМБ має три компоненти: стоксову, антистоксову та незміщену (рис. 2.5). Незміщена компонента в спектрі розсіювання відповідає процесам релеївського розсіювання. Спектральна відстань ∆ω між компонентами в спектрі РМБ перебільшує ширину релеївської лінії й залежить від кута розсіяння . При малих кутах розсіювання ( → 0, розсіювання "вперед") ∆ω→ 0. При великих кутах розсіювання ( → π , розсіювання "назад") ∆ω можна знайти з умови k_а = 2k , а саме:

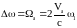, (2.6)

що збігається з доплерівським виразом (2.2) при = π .

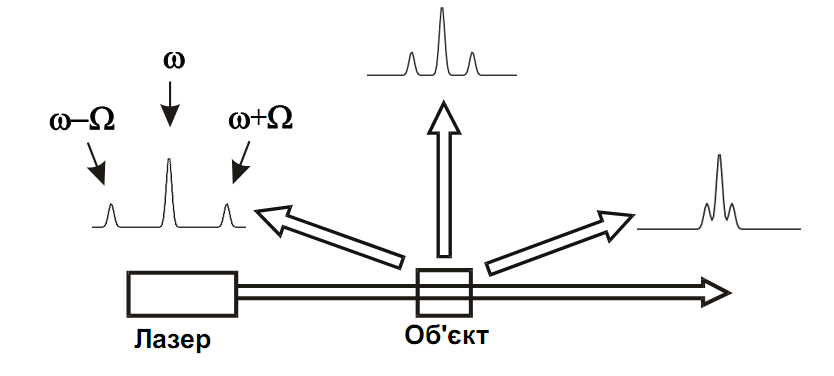
Рис. 2.5. Залежність спектра РМБ від кута розсіювання.

Відзначимо суттєву відмінність РМБ від розсіювання Рамана (комбінаційного розсіювання). Раманівське розсіювання можливе як на внутрішньо-молекулярних коливаннях, так і на колективних збудженнях кристалів – на оптичних фононах. Оскільки закон дисперсії для оптичних фононних гілок можна апроксимувати Ω(k)≈const, то при розсіюванні Рамана спектральне положення стоксових та антистоксових компонент не залежить від кута розсіювання.

На експерименті практично неможливо спостерігати РМБ "вперед", оскільки цьому заважає потужне випромінювання збуджуючого лазера. Реально на практиці спостерігають РМБ на великі кути = π/2...π. За допомогою виразу (1.6) можна оцінти частоту акустичних хвиль, що беруть участь у розсіюванні "назад". Нехай ω = 10¹⁴–10¹⁵ с⁻¹. Тоді частота акустичних хвиль Ω буде належати діапазону 10⁹–10¹⁰ с⁻¹ для рідин і 10¹⁰–10¹¹ с⁻¹ для твердих тіл.

Як схематично показано на рис.2.6, у спектрі розсіюваного світла можна виділити три області. Раманівські частоти , що зумовлені розсіюванням на оптичних фононах, займають інтервал 10 – 3000 см^-1. Мандельштам – Бріллюенівські спектри, котрі виникають внаслідок розсіювання на акустичних модах, знаходяться в інтервалі 1 - 0.05 см^-1. Релеївські спектри, що зумовлені розсіюванням на модах, котрі не поширюються, знаходяться в інтервалі 10^-9 – 10^-4 см^-1. На рисунку також показані типові області значення енергії та імпульсу в різних експериментах по розсіюванню. Видно, що при оптичному розсіюванні енергія змінюється значно сильніше, ніж імпульс. Непружне розсіювання теплових нейтронів відбувається зі значною зміною імпульсу [25].

Вимірювання частотного зсуву компонент Мандельштам – Бріллюена дозволяє визначити швидкості поширення пружних хвиль, з яких можуть бути визначені пружні константи кристалів. Фотопружні константи можуть бути розраховані з вимірювання інтенсивності ліній в спектрах МБР.

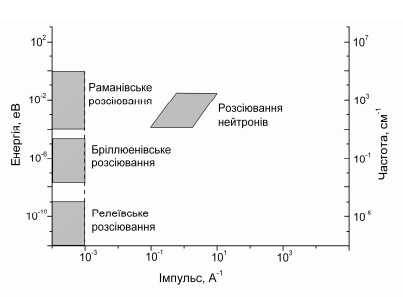Рис. 2.6. Схематична діаграма, що ілюструє область значень енергії, частоти та імпульсу, котрі перекриваються трьома експериментами по розсіюванню світла.

Розсіювання Мандельштама – Бріллюена являється потужним інструментом дослідження фізичних властивостей речовин. Крім того, за шириною ліній розсіювання можна виміряти параметри поглинання гіперзвуку в речовині. Слід також зазначити, що у твердих тілах та рідинах із високою в'язкістю спектр РМБ може містити декілька компонент, пов'язаних із повздовжніми та поперечними звуковими хвилями [26].