2.2.Тройной интеграл
2.2.1.Определение тройного интеграла
П
усть
- замкнутая пространственная область
в декартовой прямоугольной системе
координат
,
а функция
определена и непрерывна в этой области.
Разобьем область
произвольным образом на
непересекающихся подобластей с объемами
и в каждой части
выберем произвольным образом точку
.
Составим интегральную сумму:
.
Предел
интегральной суммы при
и
существует и называется тройным
интегралом от функции
по области
:
.
Если ввести
обозначения
и
,
то тройной интеграл можно записать так
.
Разобьем область
на подобласти, ограниченные плоскостями,
параллельными координатным плоскостям.
Интегральная сумма в представляет
собой сумму объемов таких областей,
если выбрать
.
Переходя
к пределу, получим, что тройной интеграл
есть объем области
.
Свойства тройного интеграла аналогичны указанным в предыдущей теме свойствам двойного интеграла.
2.2.2.Вычисление тройных интегралов
Рассмотрим
область
,
ограниченную снизу и сверху поверхностями
и
и цилиндрической поверхностью с
образующими, параллельными оси
.
Пусть
- проекция области
на плоскость
.
Предположим, что любая прямая, параллельная
оси
,
пересекает границу области
не более чем в двух точках.
Тогда для любой непрерывной в области
функции
имеет место формула
.
По этой формуле
сначала вычисляется внутренний
однократный интеграл по переменной
,
при этом
и
рассматриваются как постоянные. Затем
по изложенным в предыдущей теме правилам
вычисляется двойной интеграл. Например,
если область
задается неравенствами
,
,
то формулу можно переписать в виде
,
т.е. свести к последовательному вычислению трех определенных интегралов.
Если область не относится к рассмотренному типу, то ее всегда можно разбить на непересекающиеся части, для которых процесс сведения вычисления тройного интеграла к вычислению определенных интегралов возможен.
Следует
заметить, что пределы интегрирования
внешнего интеграла всегда постоянны.
Пределы интегрирования во внутренних
интегралах в формуле всегда переменны,
за исключением случая, когда
- параллелепипед с гранями
,
,
,
,
,
:
.
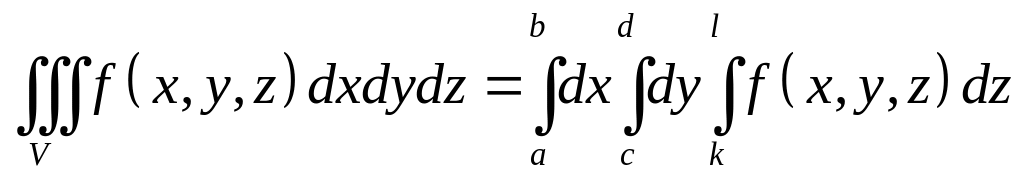Формулу можно записать в виде
,
где
- сечение области
плоскостью
.
Такая запись иногда удобнее, чем , в
особенности, если
достаточно легко описывается аналитически.
Отметим, что
формулы допускают естественные обобщения
на другой порядок интегрирования по
переменным
в кратных интегралах.
2.2.3.Переход к криволинейным координатам
Часто область интегрирования такова, что уравнения поверхностей, ее ограничивающих, удобно записывать в цилиндрических координатах. Цилиндрическая система координат является сочетанием оси декартовой системы и полярной системы координат на плоскости с полюсом в начале координат и полярной осью, совмещенной с положительной частью оси .
Произвольную
точку
в пространстве определяют три числа:
полярные координаты
и
точки
– проекции точки
на плоскость
и число
.
Декартовы
координаты
точки
и ее цилиндрические координаты
связаны формулами:
, 
,
где
,
,
,
а выбор нужного угла
из двух главных значений, даваемых
формулой
,
можно произвести по знакам координат
и
,
определяющим четверть круга, из которой
следует брать значение угла
.
Тройной интеграл в цилиндрических координатах вычисляется по формуле
,
где
– область изменения цилиндрических
координат,
.
Пределы интегрирования расставляют,
исходя из геометрического смысла
координат
и вида области
.
Особенно удобно пользоваться формулой , когда задача обладает цилиндрической (осевой) симметрией: граница области – поверхность вращения, а подынтегральная функция зависит (после перехода к цилиндрическим координатам) только от и . В этом случае
,
где
– плоская область, вращением которой
от значения полярного угла
до значения
,
вокруг оси
получена область
.
Формулу можно обобщить на случай, когда
осевая симметрия отсутствует:
.
В этом
случае вид области
зависит от угла
.
Если во внешнем интеграле проводить интегрирование по переменной , то
,
где
– сечение
плоскостью
.
В сферической
системе координат положение точки
в пространстве определяется тремя
числами: длиной
радиус-вектора, полярным углом
проекции точки
на плоскость
и углом
между радиус-вектором точки
и осью
.
Декартовы координаты
точки
и ее сферические координаты
связаны формулами:
, 
где
,
,
,
а выбор нужного угла производится, как
в случае цилиндрических координат, по
знаку координат
и
.
Тройной интеграл с сферических координатах вычисляется по формуле
,
где
– область изменения сферических
координат,
.
Пределы интегрирования расставляют,
исходя из геометрического смысла
координат
и вида области
.
Сферическими координатами особенно
удобно пользоваться в тех случаях, когда
задача имеет цилиндрическую или
сферическую симметрию. Заметим, что
угол
имеет в сферических и цилиндрических
координатах один
и тот же геометрический смысл, поэтому
справедлива формула, аналогичная :
.
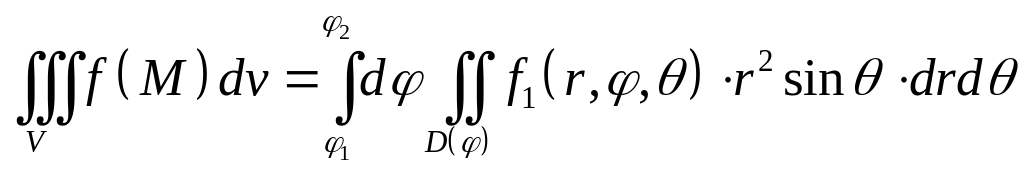Вид области
,
вообще говоря, зависит от
.
Внутренний двойной интеграл в формуле
есть по сути интеграл
в полярных координатах
,
от функции
стой лишь разницей, что угол отсчитывается
от положительного направления оси
и изменяется в пределах
.
Если задача
обладает цилиндрической симметрией,
то
и
.
В случае
сферической симметрии
.