1.6.Дифференцирование неявно заданной функции

Пусть функция задана уравнением , связывающим значение функции и аргументов, и неразрешённым относительно функции . В этом случае говорят, что функция задана неявно. Не всякое уравнение определяет некоторую функцию.

Например, уравнение не имеет действительных решений и не задает никакой функции.

Теорема “О существовании неявно заданной функции”. Если в некоторой окрестности точки функция имеет непрерывные частные производные и , кроме того частная производная в точке не обращается в 0 ( ), тогда уравнение в некоторой окрестности точки определяет , как неявно заданную однозначную функцию своих аргументов , и частные производные функции в точке вычисляются по формулам:

, , … , .

Частные случаи:

1) Неявно заданная функция одного аргумента : .

2) Неявно заданная функция двух аргументов :

.

Пример.

Найти частные производные неявно заданной функции по аргументам и :

Имеем: , .

1.7.Геометрические приложения частных производных

1.7.1.Уравнение касательной и нормальной плоскости к пространственной кривой

П усть кривая задана параметрически, т.е. , . Пусть точке соответствует значение параметра : , .

Касательной к кривой в точке называется прямая, являющаяся предельным положением секущей при (Рис. 1.4.).

Уравнение касательной к пространственной кривой в точке имеет вид:

.

Нормальной плоскостью к кривой в точке называется плоскость, проходящая через точку перпендикулярно касательной в этой точке. Уравнение нормальной плоскости:

.

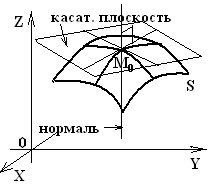
1.7.2.Уравнение касательной плоскости и нормали к поверхности

Пусть поверхность задана уравнением и пусть функция имеет непрерывные частные производные в окрестности точки , лежащей на поверхности .

Касательной плоскостью к поверхности в точке называется плоскость, в которой лежит всякая касательная, проведенная в точке к любой кривой, лежащей на поверхности и проходящей через точку .

Уравнение касательной плоскости к поверхности имеет вид:

.

Нормалью к поверхности в точке называется прямая, проходящая через точку перпендикулярно касательной плоскости.

Уравнение нормали:

.

Пример.

Написать уравнение касательной плоскости и нормали к сфере в точке .

Поверхность определяется уравнением .

Рис. 1.5.

.

Уравнение касательной плоскости:

или .

Уравнение нормали: .

1.8.Экстремум функции многих переменных

1.8.1.Необходимое и достаточное условия экстремума

Определение. Точка называется точкой максимума (минимума) непрерывной функции , если в некоторой окрестности точки , для всех точек этой окрестности выполняется неравенство: (или ). Точки минимума и максимума носят общее название точек экстремума.

Обозначим приращение функции через , тогда можно переформулировать определение экстремума:

Точка называется точкой максимума непрерывной функции , если в некоторой окрестности точки приращение функции строго отрицательно, . Аналогично, - точка минимума, если .

Теорема. «Необходимое условие экстремума функции многих переменных». Если дифференцируемая функция достигает в точке экстремума, то все частные производные функции в этой точке обращаются в 0:

.

Так как полный дифференциал функции это сумма произведений частных производных на дифференциалы аргументов, то можно сказать, что необходимым условием экстремума функции многих переменных является равенство нулю полного дифференциала этой функции в точке экстремума:

Точки, в которых выполняется необходимое условие экстремума, называются стационарными. Следовательно, если - точка экстремума функции , то либо - стационарная точка, либо в этой точке функция не дифференцируема.

Теорема. «Достаточное условие экстремума функции многих переменных». Трижды дифференцируемая в стационарной точке функция :

Имеет в этой точке экстремум, если дифференциал второго порядка функции в точке знакопостоянен и обращается в 0 только при выполнении условия: . Причем, точка является точкой максимума, если и, - точкой минимума, если .

Если дифференциал второго порядка меняет знак в окрестности , то точка не является точкой экстремума.

Если дифференциал второго порядка не меняет знак в окрестности точки , но обращается в 0 при некоторых наборах значений , среди которых есть отличные от 0, то функция в точке может иметь экстремум, а может и не иметь его ( в этом случае необходимо дополнительное исследование).