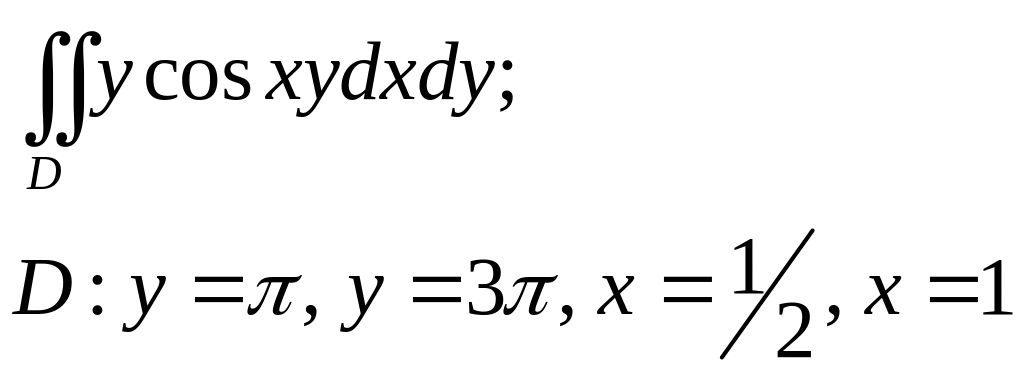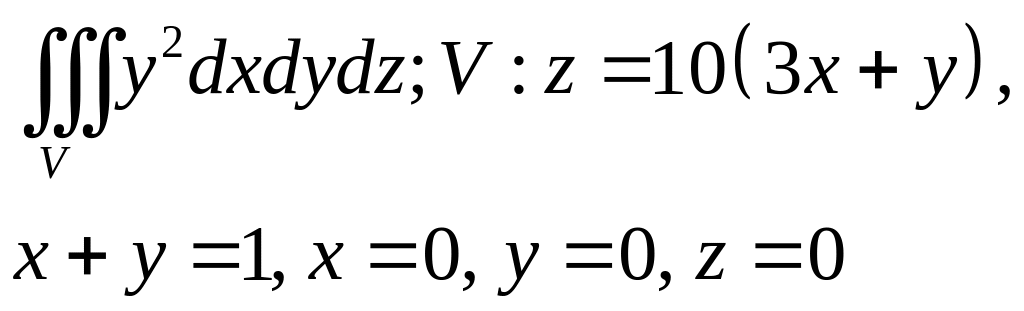- •Введение
- •1. Дифференциальное исчисление функций многих переменных 6
- •1.Дифференциальное исчисление функций многих переменных
- •1.1.Определение функции многих переменных
- •1.2.Предел и непрерывность функции многих переменных
- •1.3.Частные производные функции многих переменных
- •1.3.1.Определение частной производной и её геометрический смысл
- •1.3.2.Частные производные высших порядков
- •1.4.Полный дифференциал функции многих переменных
- •1.4.1.Необходимое и достаточное условие дифференцируемости
- •1.4.2.Применение полного дифференциала в приближенных вычислениях
- •1.4.3.Дифференциалы высших порядков
- •1.5.Дифференцирование сложной функции
- •1.6.Дифференцирование неявно заданной функции
- •1.7.Геометрические приложения частных производных
- •1.7.1.Уравнение касательной и нормальной плоскости к пространственной кривой
- •1.7.2.Уравнение касательной плоскости и нормали к поверхности
- •1.8.Экстремум функции многих переменных
- •1.8.1.Необходимое и достаточное условия экстремума
- •1.8.2.Достаточные признаки наличия экстремума для функций двух и трех переменных
- •1.8.3.Условный экстремум функции многих переменных
- •2.Кратные интегралы
- •2.1.Двойной интеграл
- •2.1.1.Определение двойного интеграла
- •2.1.2.Геометрический смысл двойного интеграла
- •2.1.3.Свойства двойных интегралов
- •2.1.4.Вычисление двойного интеграла
- •2.1.5.Замена переменных в двойном интеграле Криволинейные координаты
- •Примеры криволинейных координат Полярные координаты.
- •Обобщенные полярные координаты.
- •Выражение элемента площади в криволинейных координатах
- •2.2.Тройной интеграл
- •2.2.1.Определение тройного интеграла
- •2.2.2.Вычисление тройных интегралов
- •2.2.3.Переход к криволинейным координатам
- •2.2.4.Приложения тройного интеграла
- •3.Векторный анализ
- •3.1.Скалярные и векторные поля
- •3.1.1.Основные понятия
- •3.1.2.Геометрические характеристики полей
- •3.1.3.Дифференциальные характеристики скалярного поля Производная по направлению скалярного поля
- •Градиент
- •3.1.4.Дифференциальные характеристики векторного поля
- •Дивергенция
- •4.Контрольная работа №5
- •4.1.Пример выполнения задания:
- •5.Контрольная работа №6
- •5.1.Пример выполнения задания:
4.1.Пример выполнения задания:
1) Найти и изобразить
на плоскости
область определения функции
 .
.
Функция
![]() определена при
определена при
![]() ;
квадратный корень вычисляется из
неотрицательного числа; знаменатель
дроби не может быть равен нулю.
Следовательно, область определения
должна удовлетворять неравенствам:
;
квадратный корень вычисляется из
неотрицательного числа; знаменатель
дроби не может быть равен нулю.
Следовательно, область определения
должна удовлетворять неравенствам:
 .
.
Уравнения границ области определения есть:
 .
.
П ервые
два уравнения это уравнения прямых, а
последнее – уравнение окружности
радиуса 2. Изобразим полученные линии
на координатной плоскости, причем, если
уравнение линии было получено из строгого
неравенства, то ее следует изобразить
пунктиром (см. рис. 4.1.).
ервые
два уравнения это уравнения прямых, а
последнее – уравнение окружности
радиуса 2. Изобразим полученные линии
на координатной плоскости, причем, если
уравнение линии было получено из строгого
неравенства, то ее следует изобразить
пунктиром (см. рис. 4.1.).
Таким образом, все возможные значения переменных и разбились на семь областей. Возьмем в каждой из них произвольную точку, и подставим в систему неравенств. Если точка из области удовлетворяет системе неравенств, то и все остальные точки области будут удовлетворять этим неравенствам. В данном случае точки из областей I, V, VI, VII не удовлетворяют третьему неравенству, из области II – первому, а из области IV – второму. Таким образом, только точки области III удовлетворяют всем неравенствам системы, и принадлежат области определения функции (см. рис. 4.2.)
2) Найти частные
производные функции
 .
.
Р ассматривая
как постоянную величину, найдем
производную этой функции по
:
ассматривая
как постоянную величину, найдем
производную этой функции по
:


Аналогично, рассматривая как постоянную величину, найдем производную по переменной :


3) Найти полный
дифференциал функции
![]() .
.
Найдем частные
производные этой функции:
![]() ,
,
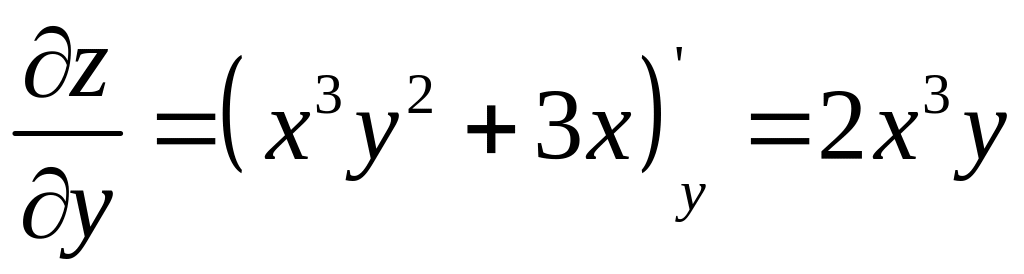 .
Тогда воспользовавшись формулой полного
дифференциала, получим:
.
Тогда воспользовавшись формулой полного
дифференциала, получим:

4) Найти частные
производные II порядка
функции
 .
Найдем частные производные этой функции:
.
Найдем частные производные этой функции:
 ,
,
 .
Продифференцировав
.
Продифференцировав
![]() второй раз по переменной
,
получим
второй раз по переменной
,
получим
 .
.
Продифференцировав
функцию
по переменной
получим
 .
(Тот же результат получили бы,
продифференцировав функцию
.
(Тот же результат получили бы,
продифференцировав функцию
![]() по переменной
).
по переменной
).
Продифференцировав
второй раз по переменной
,
получим
 .
.
5) Найти
,
если
![]() ,
где
,
где
![]() .
.
Воспользуемся формулой
![]() .
.
Здесь
 ;
;
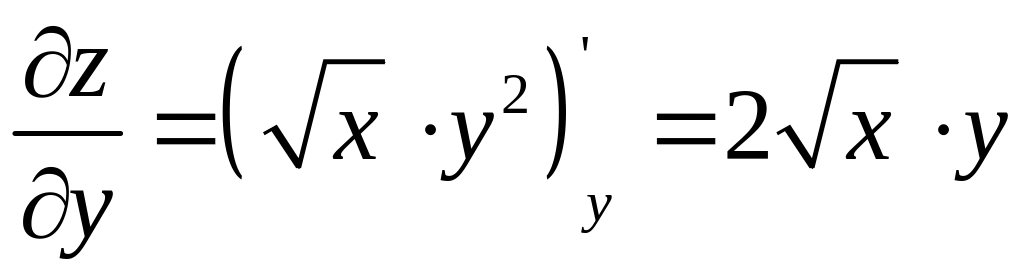 ;
;
 .
Таким образом,
.
Таким образом,
 .
.
Учитывая, что , окончательно получим
 .
.
6) Найти производную
неявной функции
![]() по переменной
.
по переменной
.
Здесь
![]() .
Продифференцируем функцию
.
Продифференцируем функцию
![]() по переменной
:
по переменной
:
 .
И по
:
.
И по
:
 .
Воспользовавшись формулой
.
Воспользовавшись формулой
 ,
получим:
,
получим:
 .
.
7) Исследовать функцию
![]() на экстремум.
на экстремум.
Частные производные
этой функции:
![]() ,
,
 .
Найдем стационарные точки этой функции,
воспользовавшись необходимым условием
экстремума:
.
Найдем стационарные точки этой функции,
воспользовавшись необходимым условием
экстремума:

Стационарная точка –
![]() .
Проверим, является ли она точкой
экстремума с помощью достаточного
условия:
.
Проверим, является ли она точкой
экстремума с помощью достаточного
условия:
 ;
;
 ;
;

В точке
![]() .
Так как
.
Так как
![]() ,
,
![]() ,
,
то точка является точкой максимума.
5.Контрольная работа №6
Задание:
Изменить порядок интегрирования.
Вычислить двойной интеграл.
Найти площадь фигуры, ограниченной данными линиями.
Вычислить тройной интеграл.
Варианты заданий представлены в таблице 1.
Таблица 1
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|
|
|
|
|
1. |
|
1. |
|
2. |
|
2. |
|
3. |
|
3. |
|
4. |
|
4. |
|